1 问题提出
随着我国经济由高速增长转向高质量发展阶段,科技创新在转变经济发展方式和优化产业结构中发挥重要作用。近年来,各地区在增加创新投入的同时,积极改善生态环境、交通基础设施、公共服务等,以期通过构建创新创业生态加速研发要素在本地区流动,而人才、资金、技术等创新要素在区域间的有序高效流动是缩小区域创新能力差距的必要条件(冯南平,魏芬芬,2017)。相较于传统的生产要素,研发要素本身携带了更多的知识和技术,特别是人力资本在区际流动,有助于加快隐性知识在更大范围内的传播和扩散[1],有利于形成区域研发合作网络,通过技术创新溢出和网络效应提升区域整体创新效率。
目前学界关于创新效率的研究主要分为三方面:一是创新效率评价,主要分为参数法和非参数法,前者通过设立随机前沿生产函数(SFA)测算创新效率。如于明洁等[2]采用参数SFA方法计算了区域创新效率;后者则运用指数法和数据包络分析法(DEA)测算创新效率。由于DEA是基于多投入多产出的评价,其结果更加客观准确,因此采用该方法的研究较多。如Guan 和 Chen[3]利用两阶段DEA 模型对高新技术企业产出效率进行评价;颜莉[4]将主成分分析法和DEA相结合,对区域创新效率进行评价;杨有才等[5]采用DEA-Malmquist指数法测算了我国高技术产业技术创新效率,并将效率分解为技术效率和技术进步。二是关于创新效率的影响因素。很多学者如金怀玉和菅利荣[6]、桂黄宝[7]、李政等[8]的实证研究结果表明,包括劳动力、FDI等创新投入均对创新效率产生重要作用,但创新投入与创新效率之间并非呈简单的线性关系[9]。此外,有学者从整体视角分析创新生态系统对创新效率的影响。如刘志春和陈向东[10]通过分析科技园区创新生态系统对创新效率的影响,认为该影响主要存在于短期,2年以上作用不显著。三是创新效率的时空演变。从宏观方面,刘军等[11]研究发现,我国协同创新效率在地理分布上呈现出明显的空间异质性;进一步地,吴芹和蒋伏心[12]指出,只有江苏、浙江和广东在知识创新效率、技术研发效率和成果转化效率方面均处于高水平,中西部地区技术研发效率较低;也有学者以长江经济带等典型区域为研究对象,分析创新效率时空演变规律[13]。从微观方面,李晓龙等[14]分析发现,高技术企业创新效率形成了以北京和江苏为中心的高值集群区。
综上,学界有关创新效率的研究较丰富,但多数是基于非流动要素的创新效率实证研究。高铁开通使得地理上的时空距离被大大压缩[15],产生了明显的时空压缩效应,提高了地区间交流的便利性[16],特别是研发人员流动有利于沟通、交流、学习和分享创新知识[17]。因此,研究由高铁开通引致的时空压缩是否改变研发要素流动对区域绿色创新效率的影响效应具有一定理论价值。此外,研发要素流动对绿色创新效率的影响是否受调节变量的影响?不同变量的阈值条件是什么?在不同调节变量作用下,研发要素流动对绿色创新效率的影响存在多大差异?这些问题目前仍未得到充分回答。本文将对上述问题展开讨论,理清时空压缩背景下研发要素流动影响绿色创新效率的本质规律,进而通过发挥高铁建设优势,带动研发要素流动,提升地区绿色创新效率。
2 影响机理
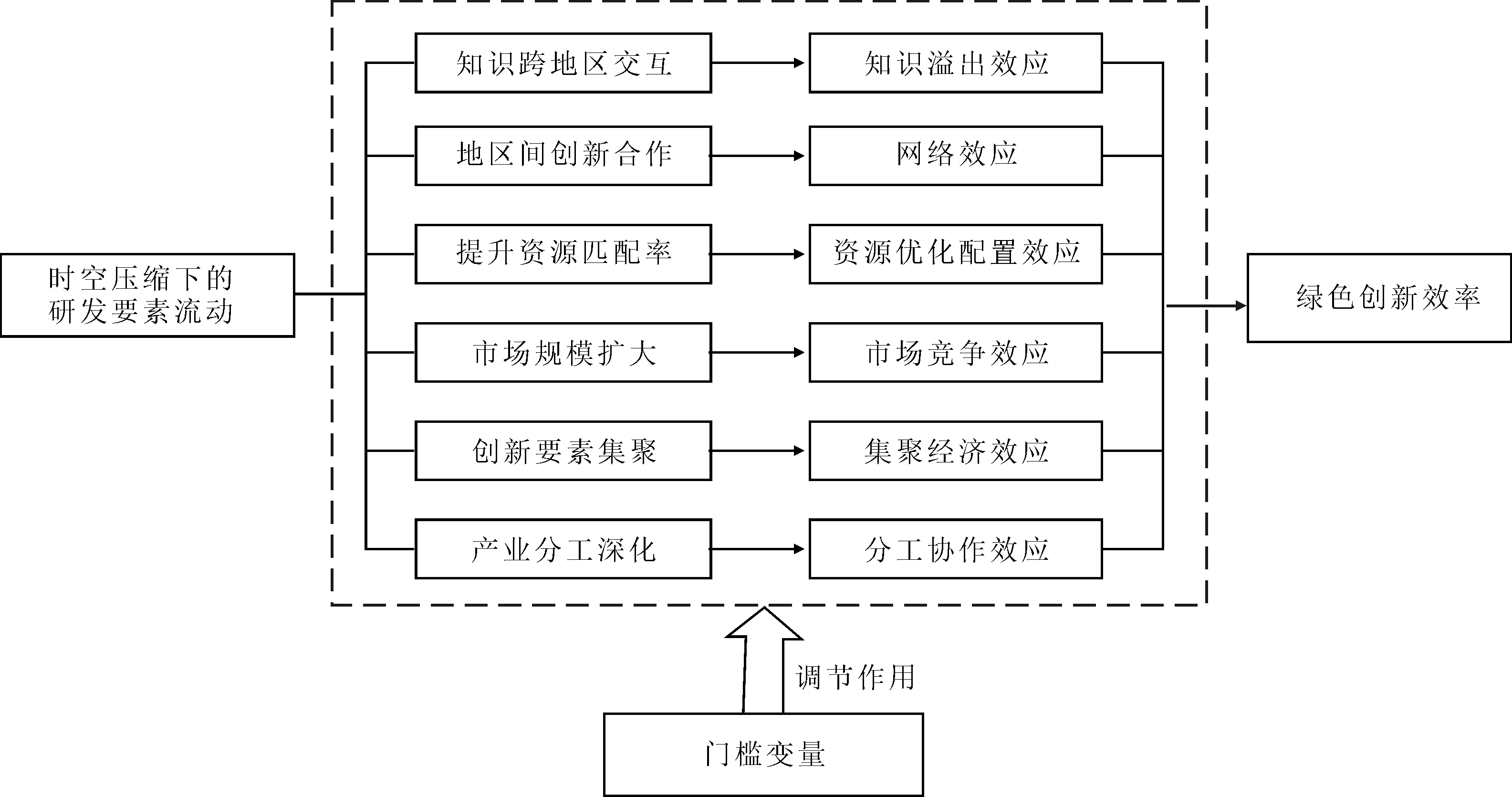
交通基础设施的完善不仅有助于增强地区间联系,更重要的是促进生产要素,特别是承载创新型知识的研发要素流动,这也是区域知识空间溢出的根本原因[18]。高铁开通极大缩短了地区通勤时间,产生了显著的时空压缩效应[19]。总体来说,时空压缩下研发要素流动对绿色创新效率的影响主要表现为:一是知识溢出效应。高铁开通极大促进了研发要素,特别是高素质人才在地区间的流动,从而有利于技术、管理等多方面知识跨地区交互与传播,通过知识溢出效应对绿色创新效率产生积极影响。二是网络效应。高铁开通使得大规模、高效和频繁的科技人才面对面交流成为可能,有利于地区间创新主体合作并构建研发合作网络,而研发网络的形成和完善有利于加快绿色创新与提高成功率,进而促进绿色创新效率提升[20]。三是资源优化配置效应。高铁开通有助于研发要素在更大空间范围内流动,降低需求企业或者创新组织间的信息不对称,提升需求端与供给端的匹配率[21],促进闲置资源参与创新,提高资源利用率[22],同时,有助于提升企业信息发布质量,缓解企业创新面临的融资约束和降低企业监督成本[23]。四是市场竞争效应。高铁开通使得企业面临的市场规模扩大,提升了竞争强度,有利于促进企业向绿色创新效率高的企业学习,通过市场竞争效应推动区域绿色创新效率提升。五是集聚经济效应。研发要素流动加速了知识在地区的集聚,而集聚外部性有助于本地区创新主体以较低成本获取外部创新资源,提升研发人员效率[24],在一定程度上弥补自身研发经费或技术不足,进而降低研发风险,促进本地区绿色创新效率提升和地区产业转型升级[25-26]。六是分工协作效应。高铁建设改变了原有区位条件和地区联系强度,更有利于高铁网络中心城市发挥扩散效应,进而促进城市专业化分工,通过分工协作提升绿色创新效率[27]。与其它交通方式不同,我国高铁系客运专线,通过人员流动,特别是研发要素的跨地区流动对绿色创新效率产生重要影响。因此,本文提出研究假设。
H1:相较于其它空间因素,因高铁开通引致的研发要素流动对绿色创新效率的影响更显著且存在空间溢出效应。
然而,一方面,从研发要素类别看,高铁开通有助于提高地区人员流动性,而研发资本流动是以人为载体的,由于高附加值的创新活动依赖于面对面的接触[28],因此因高铁开通引致的研发要素流动对绿色创新效率的影响为正向,其中,研发人员流动对绿色创新效率的影响更显著。另一方面,从高铁线路和研发资源禀赋的空间分布看,我国高铁线路呈现非均衡性,地区间差异较大,整体表现为东密西疏特征。同时,由于创新资源禀赋分布不均,地区绿色创新效率差异明显。因此,由高铁开通后时空压缩效应引致的研发要素流动对绿色创新效率的影响存在空间异质性。因此,本文提出研究假设。
H2:研发要素流动对绿色创新效率的影响为正向,从要素类别看,研发人员流动对绿色创新效率的影响更显著;从区域位置看,东部地区的绿色创新效率提升更显著。
此外,无论是研发人员流动还是研发资本流动,其对绿色创新效率的影响均可能受到多种变量的调节作用。原因在于,一方面,虽然研发人员流动有利于增强地区人才交流,进而对区域绿色创新效率产生正向影响,但研发人员过度流动也可能导致资源拥挤,不利于区域创新效率提升[29]。因此,研发要素流动对绿色创新效率的影响可能表现出一定门槛特征,低于或者高于门槛值的研发要素流动可能并不利于绿色创新效率提升。另一方面,研发人员流动对绿色创新效率的影响可能受政府财政科技支出、交通可达性、市场化程度等因素的调节。原因在于,政府财政科技支出增加有利于改善区域创新环境,更充分地发挥研发要素流动的正向效应,促进区域协同创新效率提升[30];交通可达性的改善有利于地区间合作创新[31],进而提高研发要素流动的协同创新效应;市场化程度提升有助于促进研发要素由低效部门流向高效部门,通过优化资源配置调节研发要素流动对绿色创新效率的影响[32]。因此,本文提出研究假设。
H3:研发要素流动对绿色创新效率的影响存在非线性作用关系,并受多种变量的调节。
基于上述分析,构建本文的概念模型如图1所示。
3 研究设计
3.1 模型构建
本文拟构建一个同时包含空间相关性和时间动态性的动态空间面板杜宾模型,具体为:
Yit=α+τYit-1+ηWYit-1+ρWYit+βXit+θWXit+ξt+μi+uit
(1)
其中,Yit表示被解释变量,Yit-1表示被解释变量在时间上的滞后项,WYit表示被解释变量在空间上的滞后项,WYit-1表示被解释变量在时间和空间上的滞后项,Xit表示解释变量,WXit表示解释变量在空间上的滞后值,uit为随机误差项,ξt表示时间固定效应,μi表示空间固定效应,τ、ρ、η、β和θ均为待估参数。
此外,LeSage & Pace[33]指出,使用空间回归模型可能导致结果偏误,从而提出使用偏微分方法检验与解释存在的空间溢出效应。因此,本文采用偏微分方法,将研发要素流动对绿色创新效率的影响效应分为总效应、直接效应和间接效应。上述空间杜宾模型可改写为:
Yi=(I-ρW)-1(Xiβ+WXiθ)+R
(2)
其中,R是包括截距和误差项的剩余项。对于从单位1到N的第k个解释变量,X对应的被解释变量Y的期望值偏导数矩阵可以写成:

(3)
直接效应用于测度解释变量每变化一个单位对本地区被解释变量的影响程度,由式(3)右边的偏导数矩阵对角线元素均值反映;间接效应(或称为溢出效应)用于测度解释变量每变化一个单位对邻近地区被解释变量的影响程度,由式(3)右边的偏导数矩阵非对角线元素行和或者列和均值反映。
为进一步检验研发要素流动对绿色创新效率的影响是否受调节变量的影响,以及不同调节变量门槛值带来的差异性,本文借鉴Hansen提出的门槛模型。该模型的优越性在于不仅可以估计具体门槛值,还能对内生性的门槛特征进行显著性检验。因此,在式(1)的基础上,首先假设存在单一门槛效应并建立单一门槛模型(4),然后将其扩展到双重门槛模型(5),具体模型形式如下:
Yit=α+β1Xit+γ1Vit·I(Zit≤λ1)+γ2Vit·I(Xit>λ2)+εit
(4)
Yit=α+β1Xit+γ1Vit·I(Zit≤λ1)+γ2Vit·I(Zit≤λ2)+γ3Vit·I(Zit>λ3)+εit
(5)
其中,Zit为门槛变量,I(g)为指标函数,λ1、λ2和λ3为待估算的门槛值。
3.2 变量选择与数据说明
被解释变量:绿色创新效率。借鉴杨柏等[34]的研究,采用DEA-SBM方法对创新效率进行测算。其中,创新投入指标包括R&D全时人员当量和R&D经费资本存量,期望产出指标包括发明专利申请授权数和新产品销售收入,非期望产出包括工业废水排放量、工业废气排放量和工业二氧化硫排放量。
核心解释变量:研发要素流动,具体包括R&D人员流动(RPF)和R&D资本流动(RCF)。采用引力模型对地区间RPF和RCF进行测算,具体计算公式如下:
(1)RPF测度。假设从i地区流动到j地区的R&D人员数量为RPFij,则:

(6)
其中,R&DPi为地区i的R&D人员数量,以R&D人员全时当量表征,wagei和wagej分别为i地区与j地区的城镇单位就业人员平均工资,housei和housej分别为i地区与j地区的商品房平均销售价格,Rij为地区距离;b为距离衰减指数,取值为2。i地区R&D人员流动总量如下:

(7)
(2)RCF测度。选取地区企业利润率(rate)差值和政府消费支出占GDP的比值(C)表征吸引力变量。假设从i地区流动到j地区的R&D资本为RPFij,则

(8)
其中,R&DEi为i地区的R&D资本存量,ratei和ratej分别为i地区与地j区的企业平均利润率,Ci和Cj分别为i地区与j地区的政府消费支出占GDP的比值,其它含义同上。i地区的R&D资本流动总量如下:

(9)
除核心解释变量研发要素流动外,还存在其它影响变量。参考现有研究,将外商直接投资[35]、政府财政[33]、基础设施水平[34]和市场化程度[35]作为控制变量。其中,外商直接投资选取各地区实际利用外商投资额(FDI)表征;政府财政对绿色创新效率的影响选取政府财政科技支出额(GOV)作为衡量指标;基础设施水平选取各地区人均公路里程数(ROAD)进行测度;市场化程度则以各地区技术市场成交额与科技活动经费支出比(MAR)作为衡量指标。
3.3 空间权重矩阵
本文构建基于距离标准的两类空间权重矩阵:①地理距离,以各地区省会城市(直辖市)间的欧氏距离表征;②时间距离,以各地区省会城市(直辖市)间的通勤时间表征,包括高速公路、普通铁路和高速铁路3种交通方式。
3.4 数据说明
研究期为2001—2018年,采用我国内地31个省级行政区面板数据,其宏观经济数据来自相应年份的《中国统计年鉴》《中国科技统计年鉴》以及各地区统计公报等。各地区地理距离通过ArcGIS软件计算得出,高速公路通勤时间基于百度地图以地区间最短高速公路里程除以最快限定时速计算得出,而普通铁路和高速铁路通勤时间则通过中国铁路客户服务中心网站逐条查找省会城市或直辖市之间的最短铁路运行时间,没有直达车时按最短换乘时间表征。为避免数据的非平稳性,本文实证分析所用数据均取自然对数,然后建模回归。另外,考虑到绿色创新效率可能存在一定时滞,以其滞后1期数据进行分析。
4 实证结果分析
4.1 基准结果分析
在利用空间面板模型实证分析研发要素流动对绿色创新效率的影响时,首先对创新的空间相关性进行检验,而Moran′s I指数是常用的测度指标,其具体计算公式如下:

(10)
其中,n是研究单元数量,xi和xj分别代表地区i与地区j的专利授权量,S2表示xi和xj的协方差。Moran′s I指数值若为正,则表示属性值空间正相关;若为负值,则表示属性值空间负相关;如为零值,则表示不存在空间相关性。表1为2011—2018年基于地理、高速公路和高速铁路3种距离的地区间绿色创新效率Moran′s I指数值。
表1 不同距离下绿色创新效率Moran's I 指数值

年份地理距离高速公路时间距离高速铁路时间距离20110.359***0.334***0.408***20120.349***0.350***0.402***20130.323***0.350***0.389***20140.300**0.360***0.407***20150.293***0.335***0.398***20160.309***0.364***0.416***20170.312***0.375***0.421***20180.311***0.382***0.433***
注:*、**和***分别表示变量通过了10%、5%和1%的显著性水平检验,下同
从表1可以发现,3种距离下的绿色创新效率Moran's I指数值虽然存在一定差异,但均显著为正,且通过了显著性检验,表明我国区域绿色创新效率在整体上仍然呈现空间集聚特征,虽然在研究期内有波动,但集聚趋势未发生显著变化。
为避免使用非平稳变量建立的回归模型产生虚假回归问题,实证分析前首先对变量作平稳性检验。检验结果表明,数据是平稳的。在此基础上,采用动态面板模型进行回归分析,检验被解释变量滞后项和残差序列的空间相关性,确定空间计量模型形式。由基准模型得到的研发要素流动对绿色创新效率影响的估计结果如表2所示。
表2 普通面板模型估计结果
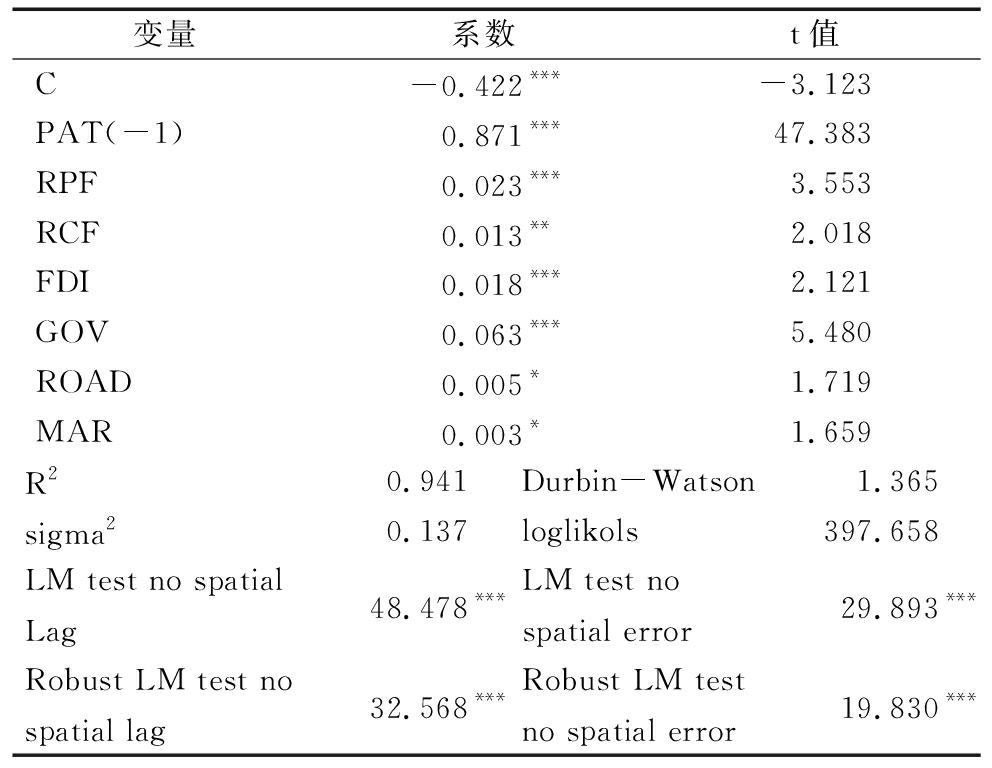
变量系数t值C-0.422***-3.123PAT(-1)0.871***47.383RPF0.023***3.553RCF0.013**2.018FDI0.018***2.121GOV0.063***5.480ROAD0.005*1.719MAR0.003*1.659R20.941Durbin-Watson1.365sigma20.137loglikols397.658LM test no spatial Lag48.478***LM test no spatial error29.893***Robust LM test no spatial lag32.568***Robust LM test no spatial error19.830***
表2结果表明,解释变量和控制变量系数均通过了显著性检验。通过拉格朗日乘子检验(LM)发现,无论是SE-LM还是SL-LM均通过了5%水平下的显著性检验,说明被解释变量滞后项和残差序列均存在空间自相关;进一步对其进行稳健性拉格朗日乘子检验(Robust LM),结果显示,SL-RLM和SE-RLM也均通过1%水平下的显著性检验,说明同时考虑被解释变量滞后项的空间自相关和残差项的空间自相关,采用动态空间杜宾模型实证分析研发要素流动对绿色创新效率的影响是有效的。
表3报告了对存在空间效应和时间效应的空间杜宾面板模型进行LR、Wald检验的结果,进而判断SDM是否可以转化为SLM或SEM。
表3 统计量检验结果

变量统计值变量统计值Wald_spatial_lag26.604***LR_spatial_lag23.124***Wald_spatial_error19.788***LR_spatial_error23.252***Hausman test96.610***
由表3可知,无论是LR检验还是Wald检验,均拒绝原假设,即SDM不能转化为SLM或SEM。同时,Hausman统计值为96.610,通过了1%的显著性检验,拒绝真实模型为个体随机效应模型的原假设。综上所述,本文将采用时空双固定的空间杜宾面板模型研究研发要素流动对绿色创新效率的影响及其空间效应。为避免估计结果有偏、单一研究时段与空间权重矩阵可能导致估计结果出现偶然性,采用偏微分方法计算不同空间权重矩阵和研究时段的效应分解结果,具体如表4所示。
表4 效应分解估计结果

空间权重(1)地理距离(2)时间距离(高速公路)(3)时间距离(普通铁路)(4)时间距离(高速铁路)变量2001-20182001-20182001-20102011-2018直接效应PAT(-1)0.867***(44.305)0.764***(27.111)0.731***(45.502)0.755***(44.931)RPF0.029*(1.927)0.057***(2.467)0.045***(2.735)0.075***(2.853)RCF0.017*(1.934)0.038**(2.435)0.032***(2.686)0.052**(2.370)FDI0.011**(1.993)0.006*(1.792)0.014*(1.876)0.012*(1.745)GOV0.049***(3.327)0.078**(2.461)0.051**(2.146)0.059***(3.091)ROAD0.008**(2.224)0.013**(2.037)0.023**(1.988)0.021**(2.379)MAR0.004**(2.273)0.005**(2.299)0.007**(2.073)0.011**(2.038)间接效应PAT(-1)0.024*(1.769)0.164**(2.153)0.105*(1.869)0.177**(1.972)RPF0.001(0.970)0.018*(1.744)0.041*(1.814)0.066*(1.871)RCF0.001(1.183)0.013*(1.921)0.029*(1.925)0.034*(1.693)FDI0.001**(2.105)0.025(0.138)0.056(1.283)0.070(0.940)GOV-0.011*(-1.705)-0.003**(-2.286)-0.006**(-2.151)-0.008**(-2.035)ROAD0.002**(2.105)0.025*(1.892)0.013***(2.618)0.034***(2.977)MAR0.001*(1.834)0.050*(1.877)0.026*(1.732)0.013*(1.716)总效应PAT(-1)0.891***(39.881)0.928***(39.881)0.836***(32.805)0.932***(37.674)RPF0.030*(1.671)0.065**(2.171)0.086**(2.239)0.141**(2.328)RCF0.018*(1.834)0.051*(1.834)0.061*(1.834)0.086**(2.183)FDI0.012**(2.186)0.031*(1.651)0.070(1.573)0.082(1.183)GOV0.038**(2.073)0.075**(1.987)0.045***(2.806)0.051**(2.482)ROAD0.010**(1.993)0.038**(1.971)0.036**(2.319)0.055**(2.554)MAR0.005***(2.017)0.055*(1.907)0.033**(1.983)0.024*(1.835)
从表4可以看出,无论是何种形式的空间权重矩阵,被解释变量的时间滞后项和空间滞后项系数均显著为正,前期的绿色创新效率会对当期产生重要影响;邻近地区的绿色创新效率提升会对本地区产生显著正向空间溢出效应。核心解释变量RPF和RCF的直接效应估计系数显著为正,且研发人员对绿色创新效率的影响效应最显著,说明研发要素流动对地区绿色创新效率具有重要影响,特别是在高铁开通后,时空压缩进一步增强了地区间联系,而研发要素流动促进了知识、技术等创新要素在更大空间内的传播,进而提升地区绿色创新效率水平。对比表4中不同估计结果发现,RPF和RCF的间接效应估计系数在地理距离权重下并未通过显著性检验,而在时间距离权重下通过了10%的显著性检验,且系数随着高铁开通得到提升,说明高铁开通增强了地区联系,而邻近地区研发要素流动加强意味着知识存量提升,地区间通勤成本降低有利于知识溢出,产生正向空间溢出效应。
从控制变量的直接效应估计系数看,外商直接投资、政府财政科技支出、基础设施水平和市场化程度均在一定程度上促进绿色创新,表明将上述变量引入模型进行实证分析具有合理性。从控制变量的间接效应估计系数看,本地区财政科技支出增加会对邻近地区绿色创新效率产生负向空间溢出效应;本地区基础设施水平和市场化程度越高,越有利于邻近地区绿色创新效率提高。
比较表5中的模型(2)和模型(4),不难发现,研发要素流动及其空间滞后项系数存在较大差异。与模型(2)相比,模型(4)中研发人员和研发资本流动对绿色创新效率的直接影响效应与间接影响效应更显著,特别是研发人员的影响。同高铁未开通相比,高铁开通带来的时空压缩效果增强了地区间联系,也提高了研发要素流动,特别是研发人员面对面交流的机会,使得知识、资本、技术等在更大范围内传播,提升了研发要素配置效率,进而提高了地区绿色创新效率。对比两种模型控制变量的间接效应估计系数发现,高铁开通带来的时空压缩效果使得研发要素在地区间快速流动成为可能,特别地,从研发人员流动空间滞后项系数看,其每提升1%会产生0.066%的正向空间溢出效应。此外,邻近地区财政科技支出对本地区绿色创新效率的负向作用更显著。可能的解释是,高铁开通引致时空压缩,一方面,增强了地区间联系,并通过知识溢出、资源优化配置等方式促进绿色创新效率提升;另一方面,区域一体化程度提升,加剧了竞争程度,特别是政府财政科技支出有利于创新要素的本地化集聚,进而对邻近地区产生不利影响。此外,在模型(2)和模型(4)中,外商直接投资的间接影响效应并未通过显著性检验。原因在于,邻近地区外商直接投资增加,一方面,可以通过相互学习加速知识溢出;另一方面,也可能导致对本地区研发要素的挤占,从而使得整体空间溢出效应未通过显著性检验。
表5 区域异质性检验估计结果

题项东部地区中部地区西部地区直接效应PAT(-1)0.758***(34.931)0.861***(46.453)0.755***(44.931)RPF0.105**(2.579)0.079**(2.382)0.057***(2.664)RCF0.073**(2.321)0.065**(2.339)0.082***(3.312)FDI0.009(1.543)0.013**(2.105)0.054**(2.366)GOV0.046***(2.523)0.104**(2.247)0.160*(1.851)ROAD0.022**(2.054)0.015*(1.643)0.014**(2.476)MAR0.022**(2.031)0.011**(2.076)0.003*(1.647)间接效应PAT(-1)0.203**(2.091)0.127**(2.192)0.098*(1.678)RPF0.098*(1.834)0.182*(1.745)0.121(1.191)RCF0.039*(1.621)0.143*(1.764)0.127(1.196)FDI0.058***(3.637)-0.068***(-2.685)-0.035(-0.143)GOV-0.034***(-3.332)0.044***(2.702)0.035(0.531)ROAD0.001**(2.006)0.023**(2.017)0.012***(2.761)MAR0.001*(1.675)0.013*(1.865)0.014**(2.021)总效应PAT(-1)0.961***(30.674)0.988***(38.461)0.853***(33.809)RPF0.203**(2.203)0.261**(2.113)0.178**(2.405)RCF0.112*(1.871)0.208**(1.983)0.209***(2.751)FDI0.067**(2.106)-0.055**(-2.332)0.019*(1.815)GOV0.012**(2.331)0.148**(2.412)0.195*(1.682)ROAD0.023**(2.013)0.038*(1.916)0.026**(2.354)MAR0.023*(1.871)0.024**(1.961)0.017*(1.933)
模型(2)和模型(4)是基于不同研究周期和空间权重矩阵得出的估计结果,单纯对比两种回归结果发现,由于绿色创新效率处于不同阶段,因高铁开通引致的时空压缩下研发要素流动对绿色创新效率的影响存在一定偏差。为充分说明时空压缩下研发要素流动对绿色创新效率的重要作用,基于不含高铁的时间距离对2001—2010年数据进行回归分析,得到表4中的模型(3)。通过对比模型(4)中核心解释变量研发人员和资本流动对绿色创新效率影响的估计系数发现,高铁开通后,无论是直接效应还是间接效应,研发要素流动对绿色创新效率的影响均更显著,进一步印证时空压缩下研发要素流动对绿色创新效率具有重要推动作用。从控制变量的估计系数看,高铁开通后FDI对绿色创新效率的直接效应减弱。高铁开通增强了地区间联系,降低了对外商直接投资的依赖,而政府财政科技支出和市场化水平对绿色创新效率的影响进一步提升,说明当距离不再是问题时,地方财政科技支出和市场化水平提升优化了本地区创新环境,进而吸引更多创新要素向本地区集聚,促进了绿色创新效率水平提升。
4.2 区域异质性检验
我国不同地区的科技资源禀赋和创新能力存在较大差异,如东部地区创新较为活跃,而高铁线路整体上也呈现出东密西疏的空间分布特征。这使得高铁开通一方面可能导致研发要素进一步向东部地区集聚,产生负向空间溢出效应;另一方面,中西部地区间联系密度增大,从而有利于获取异质性信息,进而促进本地区创新水平提升。为分析时空压缩下研发要素流动对不同地区的直接效应和间接效应是否存在差异性,本文将样本划分为东部、中部和西部,分别按照式(1)进行回归。
表5为时空压缩下研发要素流动对我国东部、中部和西部绿色创新效率的影响效应。结果显示,研发要素流动对绿色创新效率的影响不仅存在要素异质性,还存在地区异质性。从东部地区研发要素流动对绿色创新效率的影响看,RPF直接效应和间接效应的估计系数均显著大于RCF,说明对东部地区而言,由时空压缩引致的研发要素流动对绿色创新效率具有正向促进作用,且研发人员流动的作用更显著,高于全国平均水平。从控制变量估计系数看,FDI的直接效应未通过显著性检验,而间接效应显著为正。其原因在于,对东部地区而言,整体绿色创新效率较高,创新活动越来越依靠自主知识创新,减弱了对FDI的依赖;而本地区FDI增加有利于知识和技术的跨地区传播,进而产生显著的正向空间溢出效应。与全样本回归结果相比,东部地区财政科技支出对创新的直接效应减弱,而市场化水平对绿色创新效率的促进作用显著增强。其原因在于,东部地区市场化水平较高,特别是技术市场成熟,使得市场力量对绿色创新效率的积极作用被进一步放大。此外,基础设施对绿色创新效率的直接影响显著高于全样本归回归结果,即完善的基础设施有利于东部地区内部知识、技术等创新要素流动与交互,进而促进绿色创新效率提升。
从中部地区核心解释变量的估计结果看,RPF和RCF的直接效应与间接效应均通过了显著性检验,且间接效应更显著。对中部地区而言,一方面,本地区研发要素流动增强有利于提升绿色创新效率水平;另一方面,邻近地区研发要素流动增强对本地绿色创新效率亦有促进作用,且高于全样本平均水平。其原因在于,对中部地区而言,因高铁开通带来的时空压缩有助于其加强与东部地区联系,而东部地区研发要素流动增强意味着该地区创新活动和知识存量增加,有利于中部获取异质性创新资源,进而促进本地区绿色创新效率提升。从控制变量估计系数看,外商直接投资对绿色创新效率的直接影响效应和间接影响效应均通过了显著性检验,但作用方向相反。对中部地区而言,受限于自身创新发展阶段,本地区FDI增加会显著促进绿色创新效率提升;同时,邻近地区外商直接投资增加可能造成对中部地区创新资源的虹吸效应,进而产生显著负向空间效应。政府财政科技支出对创新活动的直接影响效应在所有控制变量中最显著,验证了政府在促进中部地区绿色创新效率中的积极作用。
从西部地区核心解释变量的估计结果看,RPF和RCF的直接影响效应显著为正,而间接影响效应并未通过显著性检验。受创新发展阶段、地理因素、高铁建设不完善等众多因素影响,时空压缩下的研发要素流动对西部地区有显著促进作用;但邻近地区研发要素流动增大并不会产生显著空间溢出效应。从控制变量的估计系数看,政府财政科技支出和外商直接投资的直接影响效应显著高于全样本平均值,而基础设施和市场化水平对绿色创新效率的促进作用较弱。原因在于,对西部地区而言,整体绿色创新效率偏低,自主创新能力较弱,外商直接投资增加带来的正向促进作用大于挤占效应;同时,受经济发展水平的影响,西部地区技术市场化程度较低,绿色创新更多依靠政府投入。
进一步地,对比东部、中部和西部三大地区研发要素流动对绿色创新效率的影响可以发现,因高铁开通引致的时空压缩在整体上更有利于东部和中部地区绿色创新效率提升,对西部地区的促进作用偏弱,即东中部更能从高速铁路建设中获益,这也与实际情况基本相符。高铁线路主要集中于我国东部和中部,西部地区较为稀疏,且受自然、地理等方面因素影响,西部省会城市间距离较远,不利于研发人员跨地区流动。对比三大地区控制变量系数不难发现,东部地区绿色创新效率对FDI和政府财政的依赖性最低,前者甚至未通过显著性检验,而西部地区对上述两项指标的依赖性最强。虽然中部地区绿色创新效率对政府财政和外商直接投资有较强依赖性,但是得益于高铁开通引致的时空压缩,使得邻近地区研发要素流动对本地区产生正向空间溢出效应。其原因在于,随着东部地区自主创新能力不断提升和中部地区产业转型升级,地区间的交流与合作日趋密切,使得中部地区更容易获取来自东部知识、资本、技术等创新要素的空间溢出。相比之下,对西部地区而言,邻近地区的研发要素流动并未产生显著的空间溢出效应,绿色创新效率提升还是依靠本地区投入。
4.3 进一步研究
由上述分析可知,时空压缩下的研发要素流动与绿色创新效率关系表现为非线性。考虑到高铁客运专线的属性,研发人员流动对绿色创新效率的影响更显著。因此,采用面板门槛模型分析在研发人员流动、财政科技支出、基础设施水平和市场化程度4种调节变量作用下研发人员流动对绿色创新效率的影响。
由表6可知研发人员流动、财政科技支出、基础设施水平和市场化程度等4种调节变量的门槛效应检验结果,其中,研发人员流动表现出双重门槛特征,财政科技支出、基础设施水平和市场化程度均表现为单一门槛特征,门槛值分别为3.342、0.325和30.131。
表6 门槛效应检验结果

变量名称门槛值H0H1F值P值结论(拒绝or接受H0)研发人员流动16.851无门槛单一门槛18.6510.007拒绝17.178单一门槛双重门槛15.5040.010拒绝18.291双重门槛三重门槛5.4330.607接受财政科技支出3.342无门槛单一门槛16.6610.011拒绝4.837单一门槛双重门槛11.8010.143接受基础设施水平0.325无门槛单一门槛15.2210.001拒绝0.451单一门槛双重门槛8.1460.163接受市场化程度 30.131无门槛单一门槛17.8730.006拒绝31.925单一门槛双重门槛8.8210.257接受
在研发人员流动、财政科技支出、基础设施水平和市场化程度4种调节变量的作用下,研发要素流动对绿色创新效率的影响结果如表7中第(1)-(4)列所示。从研发人员流动门槛效应值看,研发人员流动对绿色创新效率的影响呈现双重门槛特征,当研发人员流动量小于门槛值16.851时,其对绿色创新效率的促进作用有限;当其介于门槛值16.851~17.178时,研发人员流动对绿色创新效率的影响增强;当研发人员流动量高于第二门槛值时,其对绿色创新效率的正向促进作用达到最大,进一步印证了时空压缩下研发要素流动对绿色创新效率的重要作用。从政府财政科技支出的门槛效应看,研发人员流动对绿色创新效率的影响表现为单一门槛特征,即当财政科技支出小于门槛值3.342时,研发人员流动每提升1%会引起绿色创新效率提升0.039%;而当其大于门槛值时,研发人员流动对绿色创新效率的正向促进作用进一步增强,且通过了1%水平下的显著性检验。与财政科技支出类似,在基础设施建设和市场化水平高于对应门槛值时,两者的调节作用进一步增强。
表7 研发要素对绿色创新效率的影响:门槛回归
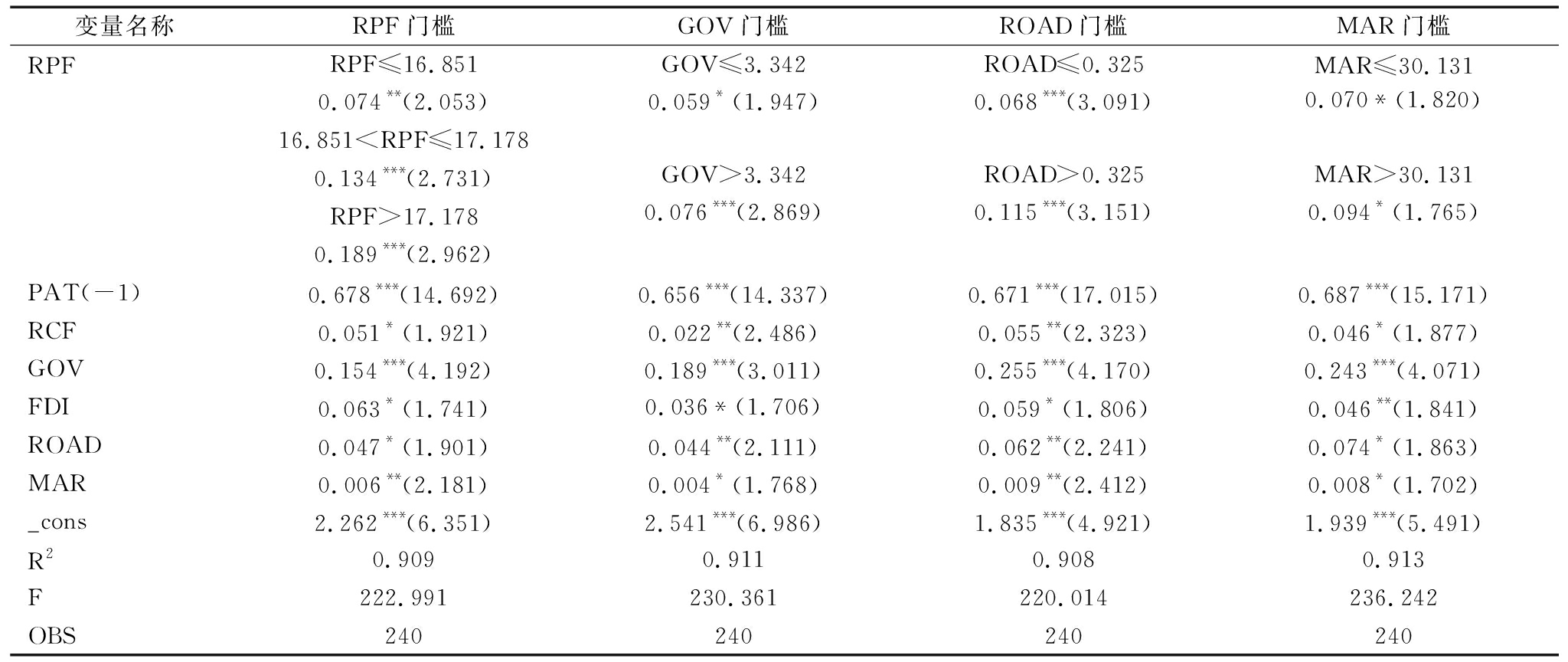
变量名称RPF门槛GOV门槛ROAD门槛MAR门槛RPFRPF≤16.8510.074**(2.053)GOV≤3.3420.059*(1.947)ROAD≤0.3250.068***(3.091)MAR≤30.1310.070*(1.820)16.8513.3420.076***(2.869)ROAD>0.3250.115***(3.151)MAR>30.1310.094*(1.765)RPF>17.1780.189***(2.962)PAT(-1)0.678***(14.692)0.656***(14.337)0.671***(17.015)0.687***(15.171)RCF0.051*(1.921)0.022**(2.486)0.055**(2.323)0.046*(1.877)GOV0.154***(4.192)0.189***(3.011)0.255***(4.170)0.243***(4.071)FDI0.063*(1.741)0.036*(1.706)0.059*(1.806)0.046**(1.841)ROAD0.047*(1.901)0.044**(2.111)0.062**(2.241)0.074*(1.863)MAR0.006**(2.181)0.004*(1.768)0.009**(2.412)0.008*(1.702)_cons2.262***(6.351)2.541***(6.986)1.835***(4.921)1.939***(5.491)R20.9090.9110.9080.913F222.991230.361220.014236.242OBS240240240240
对比财政科技支出、基础设施建设和市场化水平在研发人员流动影响绿色创新效率中的调节作用看,虽然均表现出单一门槛特征,但其贡献和显著性存在明显差异。其中,基础设施建设发挥的调节作用最大,当其跨越门槛值时,研发人员流动每提高1%将使绿色创新效率提升0.115%,显著高于财政科技支出和市场化水平,而政府财政科技支出的调节作用最小。这说明对绿色创新活动而言,虽然财政科技支出增加有利于研发要素流动,进而影响绿色创新效率提升,但相比之下,基础设施建设加大和市场化水平提高更有利于知识、技术等创新要素传播,进而充分发挥研发人员流动对绿色创新效率的正向促进作用。
5 稳健性检验
为证实前述结果的可信性,从替换被解释变量、调整控制变量和开展内生性检验三方面对上述结果稳健性进行验证,限于篇幅,只展示第一种稳健性检验结果。
5.1 替换被解释变量
由于时空压缩下的研发要素流动更注重专利应用价值,而基础研发活动较少。基于此,将期望产出中的专利授权量变为发明专利数量,通过式(1)检验研发要素流动对绿色创新效率的影响,具体如表8所示。
表8 研发要素流动对绿色创新效率的影响:稳健性分析检验结果

变量PAT(-1)RPFRCFFDIGOVROADMAR直接效应0.871***0.064**0.024**0.006*0.051***0.016*0.034**(46.453)(2.377)(2.391)(1.859)(3.446)(1.762)(2.383)间接效应0.028*0.003**0.0100.0010.002*0.004***0.002*(1.678)(2.169)(1.205)(1.196)(1.764)(2.613)(1.716)总效应 0.899***0.077**0.025**0.016*0.053***0.020**0.036**(40.063)(2.314)(2.400)(1.863)(3.577)(2.112)(2.348)
由表8可知,无论是核心解释变量还是控制变量,其系数值和显著性并未发生根本性变化。从核心控制变量看,研发要素流动的促进作用减弱,这也表明高铁开通带来的研发要素流动更多地促进了专利实用价值提升,而对原始创新的促进作用偏弱,最终导致对绿色创新效率的影响程度降低。
5.2 替换控制变量
实证分析结果表明,外商直接投资对地区绿色创新效率的影响有限。一个地区整体劳动力素质越高,越有利于吸收和转化研发要素流动带来的创新资源,进而对提升区域绿色创新效率产生重要作用。因此,考虑到地区平均劳动力素质可能带来的影响,本文以地区平均劳动力素质代替外商直接投资再进行回归,其中,以地区人均受教育年限表征劳动力素质。结果显示,在控制地区平均劳动力素质后,研发要素流动对绿色创新效率同样具有显著促进作用。
5.3 内生性检验
由于目前模型中只考虑了研发要素流动、外商直接投资、政府财政科技支出、基础设施建设和市场化水平对绿色创新效率的影响,可能导致某些重要变量遗漏,产生内生性问题。同时,受限于数据可得性,本文在测算研发要素流动时是基于引力模型,难免会造成一定误差。基于此,采用被解释变量的滞后t-2期及以上作为工具变量,采用系统广义矩估计(GMM)方法处理研发要素流动可能存在的内生性问题。动态面板模型结果显示,研发要素流动对绿色创新效率的影响效应与基准回归结果一致。
6 结论与政策建议
6.1 研究结论
本文基于高铁开通引致的时空压缩效应,结合我国内地31个省级行政单位2001-2018年面板数据,运用空间杜宾模型和面板门槛模型,探究研发要素流动对绿色创新效率的影响效应,并对4种变量的调节作用进行实证检验。研究结果发现:总体来看,高铁开通使得研发要素,特别是研发人员在地区间的大规模、快速和频繁流动成为可能,并通过人员面对面沟通与交流,极大加强了知识、技术等要素传播,通过空间溢出、优化资源配置等方式对绿色创新效率产生积极作用。高铁开通带来的研发要素大规模流动对东部和中部地区的直接影响效应更显著,且中部地区更容易接受来自东部的空间溢出,而研发要素流动对西部地区绿色创新效率的提升作用偏弱。究其原因,一方面,受经济发展阶段影响,西部地区整体绿色创新效率和质量与东中部存在较大差距,获取研发要素流动带来的异质性创新资源的能力较弱,进而限制了研发要素流动对绿色创新效率的影响;另一方面,西部省市与东中部城市距离较远,时空压缩效应不如东中部明显,因此研发要素流动量较低,对西部地区绿色创新效率的促进作用有限。此外,通过对变量调节作用的分析发现,研发要素流动对绿色创新效率的影响呈现门槛特征,且与财政科技支出、基础设施水平和市场化程度类似,4种门槛变量均呈现梯度式增强特征。
6.2 政策建议
(1)发挥东部地区绿色创新的辐射带动作用,促进地区绿色创新协调发展。对东部地区而言,特别是创新资源禀赋和能力较强的北京、上海、广州、深圳等城市,通过高铁网络建设,加强东部与中西部联系,通过构建跨区域的协同创新共享平台,加速研发人员、资本、技术等创新要素在地区间流动,提升东部对中西部地区的空间溢出效应。以高铁网络化建设加速构筑区域协同创新网络,以创新共同体建设促进区域绿色创新协调发展。
(2)加强西部与中东部地区创新合作,提升时空压缩对研发要素流动的促进作用。对西部地区而言,高铁建设虽然将西部与中东部地区连接,但因产业基础薄弱、创新环境待改善等因素影响,研发要素流动对区域创新效率的影响不如东中部显著。因此,对西部地区而言,在不断完善以高铁为代表的高速交通基础设施基础上,不断优化创新环境,充分发挥高铁建设引致的时空压缩优势,积极引导研发要素,特别是创新型人才向本地集聚,提高本地知识存量,进而内生化促进绿色创新效率提升。
(3)利用政府财政科技支出等调节变量的积极作用,放大时空压缩下研发要素流动的正向效应。在时空压缩下,财政科技支出、基础设施水平和市场化程度在研发要素流动对区域绿色经济效率的影响中均发挥正向调节作用。因此,需要各地区进一步加大政府财政科技支出,不断完善基础设施建设,持续优化市场环境,促进企业、高校等创新组织开展跨地区或跨组织技术研发活动,使知识、技术等在更大空间范围内得到传播与共享,放大时空压缩下研发要素流动对绿色经济效率的正向效应。
参考文献:
[1] 白俊红,王钺,蒋伏心,等. 研发要素流动、空间知识溢出与经济增长[J]. 经济研究,2017,52(7):109-123.
[2] 于明洁,郭鹏,张果. 区域创新网络结构对区域创新效率的影响研究[J]. 科学学与科学技术管理,2013,34(8):56-63.
[3] GUAN J C,CHEN K H. Measuring the innovation production process:a cross-region empirical study of China's high-tech innovations[J]. Technovation,2010,30(5-6):348-358.
[4] 颜莉. 我国区域创新效率评价指标体系实证研究[J]. 管理世界,2012,28(5):174-175.
[5] 杨友才,耿璐璐,史倩姿. 我国高技术产业间技术创新效率溢出效应:基于GVAR模型的研究[J]. 管理评论,2020,32(6):138-149.
[6] 金怀玉,菅利荣. 考虑滞后效应的我国区域科技创新效率及影响因素分析[J]. 系统工程,2013,31(9):98-106.
[7] 桂黄宝. 我国高技术产业创新效率及其影响因素空间计量分析[J]. 经济地理,2014,34(6):100-107.
[8] 李政,杨思莹,何彬. FDI抑制还是提升了中国区域创新效率:基于省际空间面板模型的分析[J]. 经济管理,2017,39(4):6-19.
[9] 高擎,何枫,吕泉. 产学研协同创新背景下高校科技创新效率研究:基于我国重点高校面板数据的实证分析[J]. 研究与发展管理,2020,32(5):175-186.
[10] 刘志春,陈向东. 科技园区创新生态系统与创新效率关系研究[J]. 科研管理,2015,36(2):26-31,144.
[11] 刘军,王佳玮,程中华. 产业聚集对协同创新效率影响的实证分析[J]. 中国软科学,2017,32(6):89-98.
[12] 吴芹,蒋伏心. 创新价值链下科技服务业集聚对区域创新效率的影响[J]. 中国科技论坛,2020,36(5):128-137.
[13] 杨树旺,吴婷,李梓博. 长江经济带绿色创新效率的时空分异及影响因素研究[J]. 宏观经济研究,2018,40(6):107-117,132.
[14] 李晓龙,冉光和,郑威. 科技服务业空间集聚与企业创新效率提升:来自中国高技术产业的经验证据[J]. 研究与发展管理,2017,29(4):1-10.
[15] 龙玉,赵海龙,张新德,等. 时空压缩下的风险投资:高铁通车与风险投资区域变化[J]. 经济研究,2017,52(4):195-208.
[16] 毛琦梁. 时空压缩下的空间知识溢出与产业升级[J]. 科学学研究,2019,37(3):422-435.
[17] OOSTERHAVEN J,ROMP W E. Indirect economic effects of new infrastructure:a comparison of Dutch high speed rail variants[J]. Tijdschrift Voor Economische En Sociale Geografie,2003,94(4):439-452.
[18] PAUL ALMEIDA,BRUCE KOGUT. Localization of knowledge and the mobility of engineers in regional networks[J]. Management Science (Journal of the Institute of Management Sciences),1999,45(7):905-917.
[19] YIN M,BERTOLINI L,DUAN J. The effects of the high-speed railway on urban development: international experience and potential implications for China[J]. Progress in Planning,2015,98:1-52.
[20] 程开明,王亚丽. 城市网络激发技术创新的机理及证据[J]. 科学学研究,2013,31(9):1399-1411,1440.
[21] GIBBONS S,MACHIN S. Valuing rail access using transport innovations[J]. Journal of Urban Economics,2005,57(1):148-169.
[22] 王钺,白俊红. 资本流动与区域创新的动态空间收敛[J]. 管理学报,2016,13(9):1374-1382.
[23] 杜兴强,侯菲,赖少娟. 交通基础设施改善抑制了审计师选择的“地缘偏好”吗:基于中国高速列车自然实验背景的经验证据[J]. 审计研究,2018,34(1):103-110.
[24] 余泳泽. 创新要素集聚、政府支持与科技创新效率:基于省域数据的空间面板计量分析[J]. 经济评论,2011,32(2):93-101.
[25] CHRISTOFFERSEN J,PLENBORG T,ROBSON M J. Measures of strategic alliance performance,classified and assessed[J]. International Business Review,2014,23(3):479-489.
[26] BOURREAU M,VERDIER M. Cooperative and noncooperative R&D in two-sided markets[J]. Review of Network Economics,2014,13(2):175-190.
[27] 乔彬,张蕊,雷春. 高铁效应、生产性服务业集聚与制造业升级[J]. 经济评论,2019,40(6):80-96.
[28] 董艳梅,朱英明. 高铁建设能否重塑中国的经济空间布局:基于就业、工资和经济增长的区域异质性视角[J]. 中国工业经济,2016,33(10):92-108.
[29] 郑万腾,赵红岩,陈羽洁,等. 技术扩散能否成为区域创新效率提升的新动能:研发要素流动视角[J]. 科技进步与对策,2020,37(21):56-63.
[30] 邵汉华,钟琪. 研发要素空间流动与区域协同创新效率[J]. 软科学,2018,32(11):120-123,129.
[31] GRILLITSCH M,NILSSON M. Innovation in peripheral regions:do collaborations compensate for a lack of local knowledge spillovers[J]. The Annals of Regional Science,2015,54(1):299-321.
[32] GANG FAN, XIAOLU WANG, GUANGRONG MA. The contribution of marketization to China's economic growth[J].China Economist,2012,7(2):4-14.
[33] LE SAGE J,PACE R. Introduction to spatial econometrics[M]. New York: CRC Press,2009:73-76.
[34] 杨柏,陈银忠,李爱国,等.政府科技投入、区域内产学研协同与创新效率[EB/OL].科学学研究: 1-14[2020-12-11].https://doi.org/10.16192/j.cnki.1003-2053.20200924.002.
[35] 田红彬,郝雯雯. FDI、环境规制与绿色创新效率[J]. 中国软科学,2020,35(8):174-183.
(责任编辑:胡俊健)
![]()