0 引言
新产品极高的市场失败率一直是困扰企业的痛点。2017年中国消费品市场推出了25 473个新产品,但70%的市场存活期不足18个月。新品的大规模死亡给企业乃至社会造成了巨大的资源浪费,如何让创新广泛持久地被市场接受,成为实业界和学术界非常关注的话题。
管理学中对创新扩散的理论研究经历了关注宏观扩散速度、微观扩散程度以及社会网络中创新扩散3个阶段,从社会网络角度探讨创新扩散是这一领域研究的最新进展,社会网络的节点特性、节点间连接强弱、网络拓扑结构以及网络效应等对创新扩散的影响得到了充分讨论,但也尚存一些局限和争议。
(1)普遍应用于创新扩散研究的小世界网络和无标度网络无法反映社交时代的人际结构特征。已有研究大多使用小世界网络或无标度网络代表真实社会网络,它们本质上属于稀疏网络 [1,2]。然而近年来,相关实证研究发现,现实中很多网络在演化过程中存在网络连边数量增长快于节点数量增长的现象,即网络变得越来越“稠密”[3-5]。动态稠密网络很好地反映了人际网络的稠密性,但这类模型尚未被引入创新扩散研究中,在很大程度上限制了发现新现象、开拓新观点的可能性。
(2)社会网络结构对创新扩散规模的影响有待进一步探索。基于小世界网络的创新扩散研究发现,网络聚集程度对创新扩散规模具有显著影响,但到底是聚集网络还是随机网络更有利于创新扩散,学术界尚存“社会强化论”和“弱连带优势论”两种解释[6,7]。也有部分研究使用无标度网络拟合现实网络,主要关注网络平均度和度分布异质性对创新扩散的影响[8],鲜有研究关注网络聚集程度对创新扩散规模的影响。实际上,真实的人际网络兼具小世界网络特性和无标度网络特性,为了更全面地了解社会网络结构对创新扩散的影响,必须同时关注网络聚集程度和网络度数特征如何影响创新扩散进程。
(3)网络效应强度差异对创新扩散规模的影响尚缺探讨。有研究探讨了网络效应对创新扩散规模的影响方向[9,10]、网络效应影响个体采纳行为的范围[11,12]、具有网络效应的产品在不同社会网络结构下的扩散阈值[13,14],但很少探讨网络效应强度对创新扩散规模的影响。网络效应强度的改变是否会对创新扩散规模产生影响?不同网络结构中网络效应强度的改变对创新扩散规模产生的影响是否相同?这些都有待进一步探讨。
(4)创新先驱者对创新扩散的影响值得讨论。创新先驱者和意见领袖对创新扩散会产生重要影响[15-17],现有研究更多关注意见领袖对创新扩散的影响[18-19]。但其实,创新先驱者是创新进入系统的“引路人”,某种程度上,没有创新先驱者的存在,就没有后续的创新扩散。
针对上述争议和局限,本文将复杂网络模型的最新成果——概率p复制增长网络(简称“p-GNC网络”)引入创新扩散研究中,使用p-GNC网络拟合个体采纳者网络,通过多智能体建模仿真方法构建创新扩散模型,探讨p-GNC网络结构(包括网络聚集程度和网络度数特征)、网络效应强度和社会系统中创新先驱者比例对创新扩散规模的影响。
1 创新扩散与创新扩散网络
创新扩散是创新经由特定渠道,随时间推移在社会成员中传播的过程[20]。研究社会网络环境下创新扩散的基本思路是使用复杂网络模型对真实社会网络进行理论化表达,以复杂网络模型的节点、节点连接关系、网络拓扑结构对创新扩散的影响代表真实社会中个体、个体间关系和人际网络结构对创新扩散的影响。本文选择p-GNC网络出于两大原因:首先,生成p-GNC网络的基本机制——部分复制机制在人类社会中大量存在。以社交网络为例,当两位个体互相结为好友时,往往会通过好友结识部分好友的好友,这个过程就是部分复制过程;其次,在不同复制概率下,p-GNC网络会呈现出稀疏、稠密两种不同形态,这有利于对比稀疏网络与稠密网络对创新扩散的不同影响效果。
1.1 p-GNC网络生成机制
p-GNC网络从一个很小的核开始,通过添加新节点实现增长。新节点加入网络后,随机与一个已有节点建立连接,并以概率p与该节点的邻节点建立连接[21]。
1.2 p-GNC网络平均聚集系数与平均度
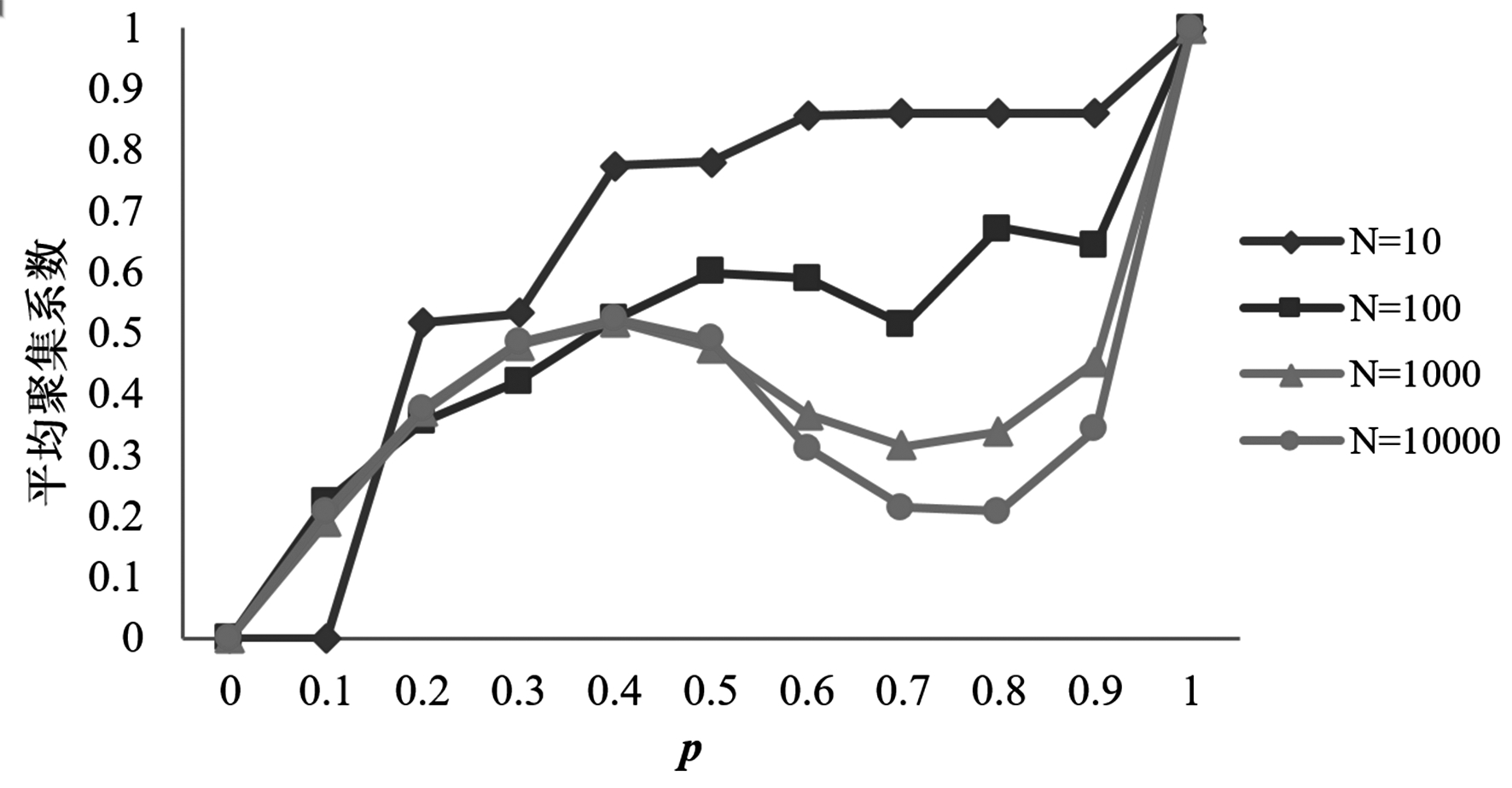
已有研究表明,网络聚集程度与平均度对创新扩散规模的影响最为显著[22-24]。因此,本文重点描述p-GNC网络的平均聚集系数与网络平均度。平均聚集系数反映了网络聚集程度。当N=10、N=100、N=1 000、N=10 000时,网络平均聚集系数与p值的关系见图1。
由图1可知,无论p-GNC网络规模多大,p-GNC网络的平均聚集系数均随着p值增加而先上升后下降,而后再上升。网络规模越小,网络平均聚集系数的上升区间越长,下降区间越短。对于大部分网络而言,网络平均聚集系数上升区间最高点在p=0.4和p=0.5附近,下降区间最低点在p=0.7和p=0.8附近。并且,网络规模越小,网络越容易达到高聚集状态,达到特定聚集程度需要的复制概率也越小。
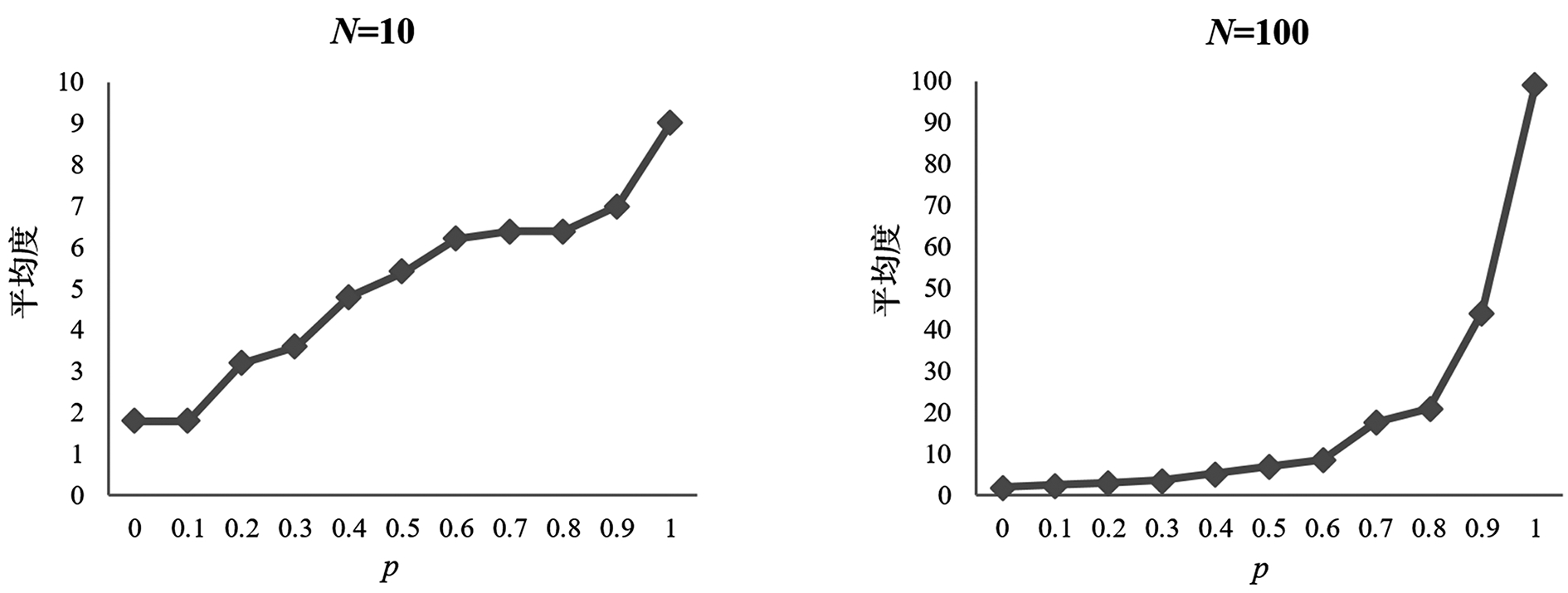
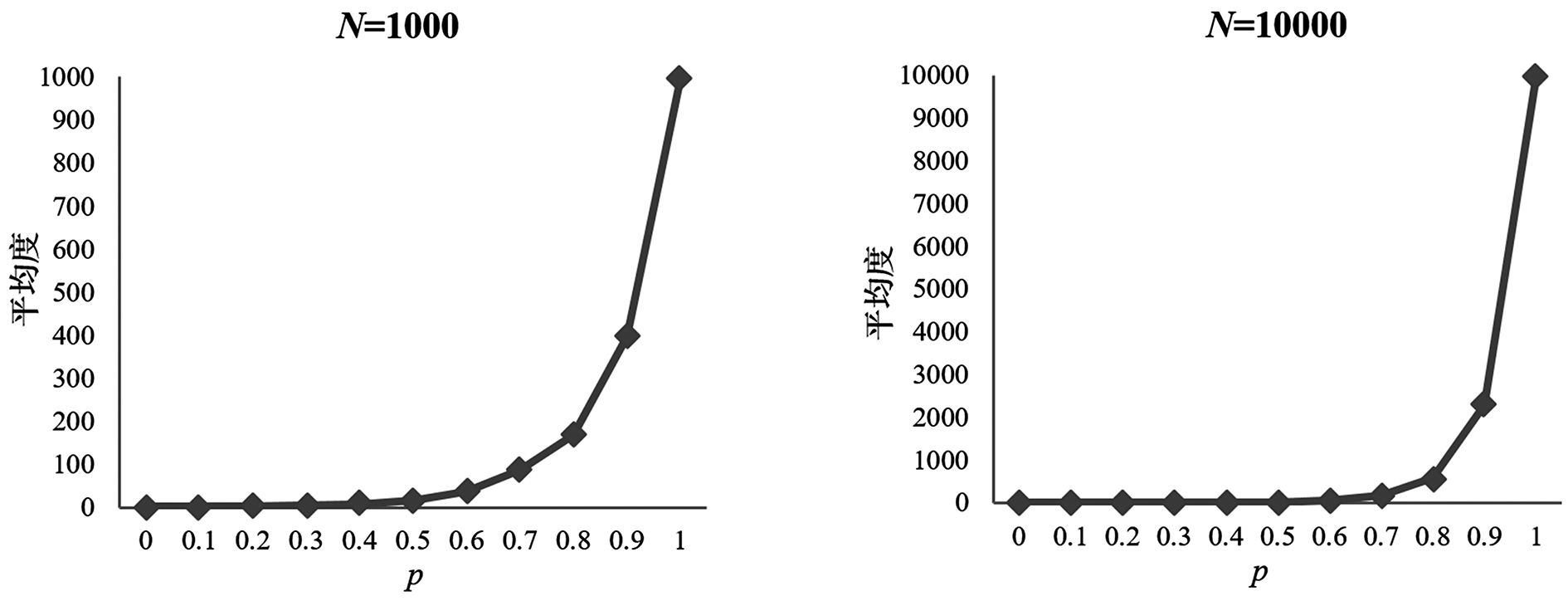
网络平均度是网络中所有节点度的均值。在N=10、N=100、N=1 000、N=10 000的不同网络规模下,网络平均度数与p值的关系见图2。
从图2可以看出,p值越大,网络平均度越大。当p<0.5时,网络平均度随网络规模增大而增加的幅度非常小,网络表现出明显的稀疏性;当p>0.5时,网络平均度随网络规模增大而超线性增加,网络表现出明显的稠密性。
2 研究假设
2.1 p-GNC网络结构对创新扩散规模的影响
(1)平均聚集系数对创新扩散规模的影响。创新扩散本质上是创新采纳行为的扩散。主流观点认为,行为扩散是一个复杂的感染过程。网络越聚集,已采纳者越容易对潜在采纳者实施多源强化,潜在采纳者实施采纳行为获得的网络效用也越高,因此,潜在采纳者越容易实施采纳决策[25]。林略和周力全[26]基于小世界网络研究了网络拓扑结构对微观采纳以及宏观扩散的影响,发现网络越聚集,创新最终累积采纳者比例越高;Centola[27]通过控制实验的方法研究了网络结构对于行为扩散的影响,发现区域聚集连接对于行为传播非常有效,聚集网络中的行为扩散更广泛。也有一些研究得出了不同结论,如黄玮强和庄新田[28]基于ER随机网络,以及娄思源[29]基于小世界网络的仿真分析均发现,网络聚集程度与稳态创新采纳比例存在非单调关系。本文依从主流观点,提出如下假设:
H1a:p-GNC网络的平均聚集系数正向影响创新扩散规模,平均聚集系数越大,创新扩散规模越高。
(2)平均度对创新扩散规模的影响。已有研究较多关注网络平均度对病毒、信息等传播效果的影响,网络平均度越大,病毒和信息的最终扩散规模越高、达到稳定状态的扩散速度也越快[30-32]。原因在于,在病毒、信息等传播过程中,一旦未感染个体与感染个体接触,就会有一定的概率转化为感染者,进而转化为传播者。个体的度数越高,接触感染个体的概率就越高,成为感染者和传播者的概率也就越高。从整个网络视角来看,网络平均度越大,传播病毒或信息的个体就越多,扩散也就越容易。然而,采纳行为的传播并不是通过简单的接触就能够传播的,个体通常基于效用函数决定是否实施采纳决策,在效用函数中,潜在采纳者的邻居中已经采纳创新的个体比例是影响个体效用的重要因素[33-34]。在扩散初期网络中存在少量采纳个体的情况下,个体平均度越大,未采纳个体的邻居中已采纳者所占比例就越低,未采纳者实施采纳行为所获得的效用也越低,从而更不容易实施采纳决策,在多次迭代之后,平均度大的网络中采纳者数量相比平均度小的网络越来越少。在相关研究中,也可以找到支持本文研究假设的一些结论,如黄玮强等[8]在无标度网络中构建了潜在采纳者采纳创新的决策函数,发现潜在采纳者关系网络的平均度值越大,创新扩散规模越小。综合上述分析,提出如下假设:
H1b:p-GNC网络的平均度负向影响创新扩散规模,平均度越大,创新扩散规模越小。
2.2 网络效应强度对创新扩散规模的影响
网络效应强度反映了邻近个体的采纳行为对个体采纳决策的影响力,其值高低与创新产品特性以及个体之间的关系强弱有关。本文重点关注由于创新产品本身特性差异带来的网络效应强度差异对创新扩散的影响,设定不同创新产品网络效应的强度不同,所有邻近个体对个体采纳决策的影响程度相同。
基于这样的前提,本文认为,网络效应强度越高,网络效应产生的效用越高,个体采纳创新获得的总效用就会越高,个体采纳创新的概率将大大提高,创新最终的扩散规模也会越大。已有研究也基本得出了相似的结论,如李凡[35]建立了基于免费商品赠送的网络效应产品扩散模型,模拟计算和实证研究结果均表明,网络效应越强,扩散达到稳定状态时的累积扩散率越高。杨珊珊[36]研究发现在随机网络、规则网络、小世界网络和无标度网络中,数字信息产品的最终采纳率都会随着网络效应强度的提高而提高;Choi等[1]认为,网络效应强度的高低对扩散初始阶段的影响尤其巨大,当网络效应强度较低时,初始阶段扩散范围明显减小,扩散失败概率也将大大提高。虽然尚未有学者研究p-GNC网络中网络效应强度如何影响创新扩散范围,但已有基于随机网络、规则网络、小世界网络、无标度网络的研究均发现,网络效应强度越大,创新扩散规模越大。因此,提出假设:
H2:在p-GNC网络中,网络效应强度正向影响创新扩散规模,网络效应强度越大,创新扩散规模越高。
2.3 创新先驱者比例对创新扩散规模的影响
根据Rogers的创新扩散理论,创新扩散采纳者经历了由创新先驱者向意见领袖波及、再由意见领袖向普通个体波及的发展过程。很显然,社会系统中的创新先驱者比例越高,促使越多的意见领袖采纳创新,意见领袖能够影响的普通个体数量也越多,创新最终在人群中的采纳比例就会越高。Truong[37]、高键等[38]研究均表明,较强的个体创新性能显著促进新产品采纳。因此,提出如下假设:
H3a:在p-GNC网络中,创新先驱者比例正向影响创新扩散规模,创新先驱者比例越高,创新扩散规模越高。
虽然普遍认为,创新扩散初期的采纳者数量越多,创新最终的扩散率也越高,但创新扩散初期采纳者数量的增加并不总能带来创新最终采纳率的同比例增加。当创新先驱者比例越来越高时,他们之间社会网络重叠率就会越来越高,这会导致创新先驱者对扩散的促进作用越来越弱,Zuncsek&Sarvary[39]将这种现象称为“饱和效应”,张磊[40]等在随机网络、规则网络、小世界网络和无标度网络中均发现了“饱和效应”的存在。虽然目前尚未有研究探讨在加速增长网络中,初始采纳者比例的提高将怎样影响创新扩散规模的扩大,不过参考以往基于稀疏网络得出的研究结论,暂且提出如下假设:
H3b:在p-GNC网络中,创新先驱者比例提高对创新扩散规模的促进作用随创新先驱者比例的增加而边际递减,创新先驱者比例越高,增加创新先驱者比例能够提高的创新扩散规模越小。
3 基于多智能体模拟仿真的创新扩散模型构建
本研究将采用多智能体建模仿真方法,从企业和个体两方面构建创新扩散模型,定义企业与个体属性、行为规则来描述创新供给与采纳过程。通过模拟计算获取数据,对本文提出的研究假设进行检验。
3.1 模型基本假设
市场由恒定数量的企业和个体构成;企业生产并出售基于特定技术的创新产品,每个企业只能生产一种产品;创新产品供应充足,创新采纳不会受到供应限制的影响;市场信息完全对称,个体知晓自身所处网络中创新产品采纳情况以及创新产品价格;潜在采纳者基于效用函数进行采纳决策,只有采纳和不采纳两种状态,同一时刻最多采纳一种创新;潜在采纳者之间仅通过口头传授相互影响,不考虑广告等大众传媒、宏观经济环境、政府政策等因素对创新采纳的影响。
3.2 企业智能体属性与行为规则
熊彼特增长理论认为,创新是生产过程中内生的,新产品或新方法的出现是由于企业存在追逐垄断利润的动机。企业通过研发生产创新获取利润,且一旦创新取得成功,就可能将其它同类企业排挤出市场,以获得垄断利润[41]。已有研究建立创新扩散模型时,往往只是简单地将创新供给视为外生的固定值或者随机变量。本文将创新供给与企业生产相结合,基于开发创新、企业成长以及企业失败退出这3类活动对企业智能体进行定义。
(1)开发创新。开发创新使企业产生研发成本和扩大生产的成本。为了保持持续竞争力,假设企业每期从可用资本中抽取一定比例的资金用于追加研发投入、扩大生产能力。可用资本越多,能够追加的研发投入就越高,但最低不得低于行业最低研发费用。令capitalt为t期企业可用资本,r为企业研发投入占可用资本比例,MinRD为行业最低研发费用,则t期企业追加研发投入为:
RDt=max{ r×Capitalt-1,MinRD }
(1)
创新的技术绩效由企业技术能力决定,令performancej,t为t期创新产品j的技术绩效,参考Lee等[42]的研究,设定performancej,t服从形状参数、尺度参数分别为(γ,Δ)、(0,ω)的β分布。其中,形状参数γ反映企业技术能力,是累积研发投入的函数[43]。令γ0为企业初始技术能力,θ为技术吸收难度,则t期企业技术能力为:
γt = γ0+ (RD0 + RD1 + … + RDt)/θ
(2)
企业每期增加研发费用,创新产品的技术绩效将逐期提高。但由于performancej,t是一个随机数,虽然E (performancej,t) >E (performancej,t-1),但在计算过程中也可能出现performancej,t-1>performancej,t的情况,很显然这种情况是不符合实际的,应当予以排除。因此,设定:
performancej,t = max{performancej,t,performancej,t-1}
(3)
企业生产能力是根据创新产品销售情况动态变化的,若t-1期生产的创新产品被社会系统中的个体全部采纳,企业将增加第t期生产能力,否则将维持t-1期的生产能力。令capacityt为t期企业生产能力,Nt为t期创新产品生产数量,nt为t期创新产品销售数量,M为每次增加的产量(M >0),则:
(4)
实践中,企业每次增加的产量可能不一样,简单起见,本文将每次增加的产量视为常数。
(2)企业成长与退出。可用资本是企业经营活动的前提。企业销售创新产品获得销售收入,增加可用资本,而企业为开发创新所进行的研发投入活动及扩张生产活动则会减少可用资本。令capitalt为t期企业可用资本,price为创新产品销售价格,Cp为企业生产创新产品边际成本,则:
(5)
当企业可用资金低于行业最低研发费用,即capitalt
(3)潜在采纳者智能体的属性与行为规则。个体是否采纳创新取决于创新为个体带来的效用,个体偏好、产品内在效用、网络效应产生的效用以及创新产品价格综合决定个体采纳创新能够获得的效用。令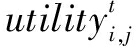 为t期潜在采纳者i采纳创新产品j获得的效用,preferencei表示潜在采纳者i的偏好,参考Lee等[42]的研究,设定preferencei服从形状参数为(β1,β2)、β1=β2、尺度参数为(-ν,0)的正态分布。个体创新性越强,尺度参数越接近0。令ai表示邻近个体对采纳者i的影响因子,installed_basedj,t表示t时刻采纳者i所处网络中使用j产品的邻近个体数量,Ki表示潜在采纳者i的邻居总数。产品价格记为price,t时的扩散规模记为φ(t)。
为t期潜在采纳者i采纳创新产品j获得的效用,preferencei表示潜在采纳者i的偏好,参考Lee等[42]的研究,设定preferencei服从形状参数为(β1,β2)、β1=β2、尺度参数为(-ν,0)的正态分布。个体创新性越强,尺度参数越接近0。令ai表示邻近个体对采纳者i的影响因子,installed_basedj,t表示t时刻采纳者i所处网络中使用j产品的邻近个体数量,Ki表示潜在采纳者i的邻居总数。产品价格记为price,t时的扩散规模记为φ(t)。
个体采纳创新,可以获得的总效用为:
(6)
当 即performancej,t+ai×installed_basej,t/ki-pricej>preferencei时,个体i采纳创新。
即performancej,t+ai×installed_basej,t/ki-pricej>preferencei时,个体i采纳创新。
4 仿真运行与分析
4.1 仿真运行步骤
在运行扩散模型前,首先需要设置模型的默认参数。企业层面的默认参数包括企业数量、企业初始资金、企业初始生产能力、企业每期追加的研发投入占可用资本的比例、企业生产产品的边际成本、企业生产产品的初始技术绩效、技术吸收难度以及技术绩效上限等;采纳者层面的默认参数包括采纳者数量、采纳者偏好分布、采纳者购买产品的价格等。其次,根据每次的研究问题改变某些变量的数值。为了尽量减小仿真运行产生的随机误差,本文设定每次参数组合模拟计算500次。每次模拟计算完成后会输出一份数据表,数据表中包含的企业层面的输出数据有企业每期销售产品数量、累积销售产品数量、企业可用资本、企业产品的技术绩效等,采纳者层面的输出数据包括平均每个个体的邻居中采纳创新产品的比例、累积采纳创新产品的采纳者数量等。最后,由于本研究模型设定产品的技术绩效是不断升级的,且网络效应不会对采纳者的效用产生负向影响,当市场只有一个产品时,给予充足的时间,产品最终一定能完全覆盖市场。单一扩散模型中,当社会网络中的全部个体都已采纳创新产品时,仿真运行终止。
4.2 仿真参数设定
为了最大程度模拟现实中的创新扩散情况,在设置扩散模型的参数数值时,应尽可能还原现实的扩散情境。本文扩散模型中涉及的参数可以分为3类:①无关紧要的参数。如潜在采纳者总数和企业数量,出于简化计算的考虑,本模型设置潜在采纳者总数1 000个,企业数量1个;②比较重要的、决定扩散模型构建与运行的假设基础是否满足的参数。例如,企业初始资金、初始生产能力、生产产品边际成本、产品价格等参数的数值要保证扩散模型“创新产品供应充足,创新采纳不会受到供应限制的影响”的前提能够成立,企业生产创新产品的技术上限值要保证“产品技术升级不会受到技术上限的限制”的前提能够成立,企业每期追加的研发投入占可用资本的比例要保证“产品技术将持续升级”的前提能够成立。经过反复调试,设定企业初始资金2 000、初始生产能力100、生产产品的边际成本50、产品价格100、生产产品的技术上限10 000、追加研发投入比例1%、行业最低研发费用50;③效用函数中涉及的、决定潜在采纳者是否会采纳创新的核心参数。包括网络结构、创新先驱者比例、潜在采纳者偏好、网络效应强度、生产产品技术的初始技术绩效、技术吸收难度等。其中,p-GNC网络的结构由复制概率p控制,由于0
4.3 仿真运行结果与分析
首先,汇总高、低网络效应强度下,创新先驱者比例分别为0%、1%、2%和3%时,不同p值下的创新采纳者数量。为了直观考察创新采纳者数量演变趋势,绘制创新扩散规模随扩散时间的演变图,见图3、图4。图3、图4显示,在不同网络效应强度、不同创新先驱者比例以及不同p值下,创新扩散规模均随时间呈“S”型变化,即依次经历起飞期、快速扩散期和稳定期。网络效应越强、创新先驱者比例越高,创新扩散的起飞期越短,创新越早进入快速扩散期,这在一定程度上支持了假设H2和假设H3a。此外,还可以看到,p-GNC网络的p值明显影响创新扩散规模,当p值较小时,创新扩散规模随p值增加而扩大;当p值大到一定程度时,创新扩散规模随p值增加而下降。为了能更细致地观察p-GNC网络结构、网络效应强度和创新先驱者比例对创新扩散规模的影响,分别截取高网络效应强度下,创新先驱者比例分别为0%、1%、2%和3%时,不同p值下创新扩散第20代和第30代的扩散数据,以及低网络效应强度下,创新先驱者比例分别为0%、1%、2%和3%时,不同p值下创新扩散第25代和第35代的扩散数据,得出创新扩散规模与p值折线图(见表1)。截取扩散数据的依据在于,在扩散早期,不同参数组合下创新扩散数据并没有非常明显的差异,这样就难以通过早期数据得到较规律的结论;而在扩散饱和或接近饱和阶段,创新在很多p值下都能达到完全扩散状态,无法精确地反映出p值对创新扩散规模的影响。经过综合比较,当ai=2 000、ai'=500时,选择第20代和第30代的扩散数据较合理;当ai=1 000、ai'=250时,选择第25代和第35代的扩散数据较合理。由图3、图4可知,创新扩散在不同代际的演变趋势基本相同。因此,截取特定代际的扩散数据代表创新在整个扩散周期内的动态变化过程是有意义的。
整体趋势而言,高强度网络效应下,无论创新先驱者比例高低,当p≤0.3时,p值越大,创新扩散规模越大;当0.3
表1 不同参数组合下创新扩散数据
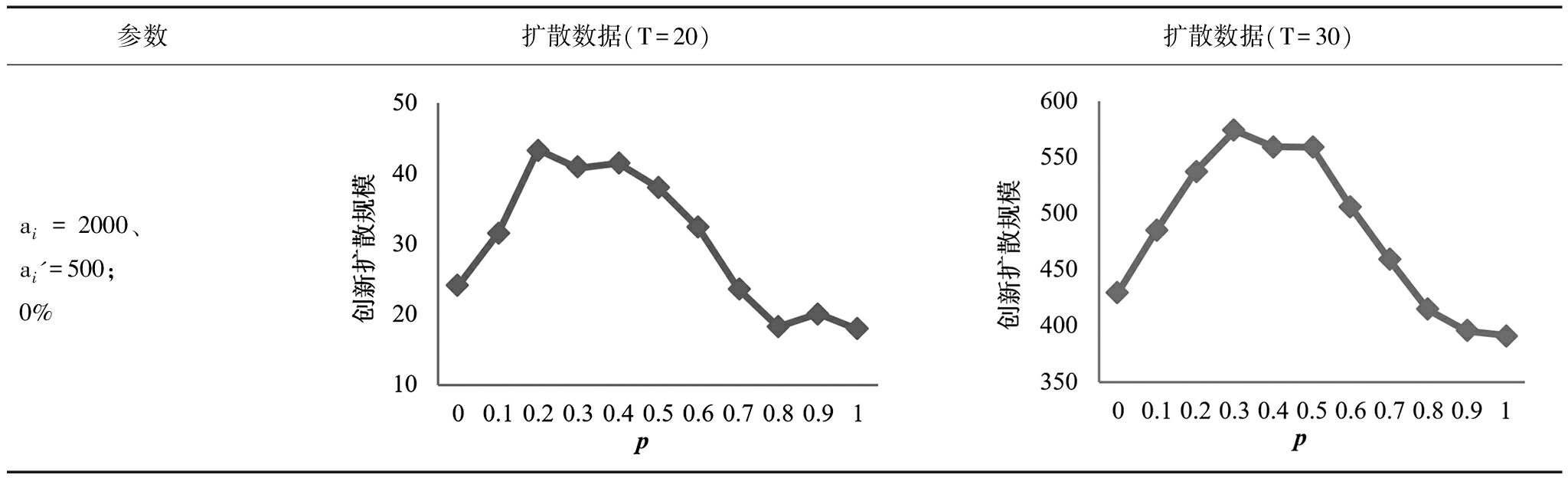
参数扩散数据(T=20)扩散数据(T=30)ai=2000、ai'=500;0%
续表1 不同参数组合下创新扩散数据
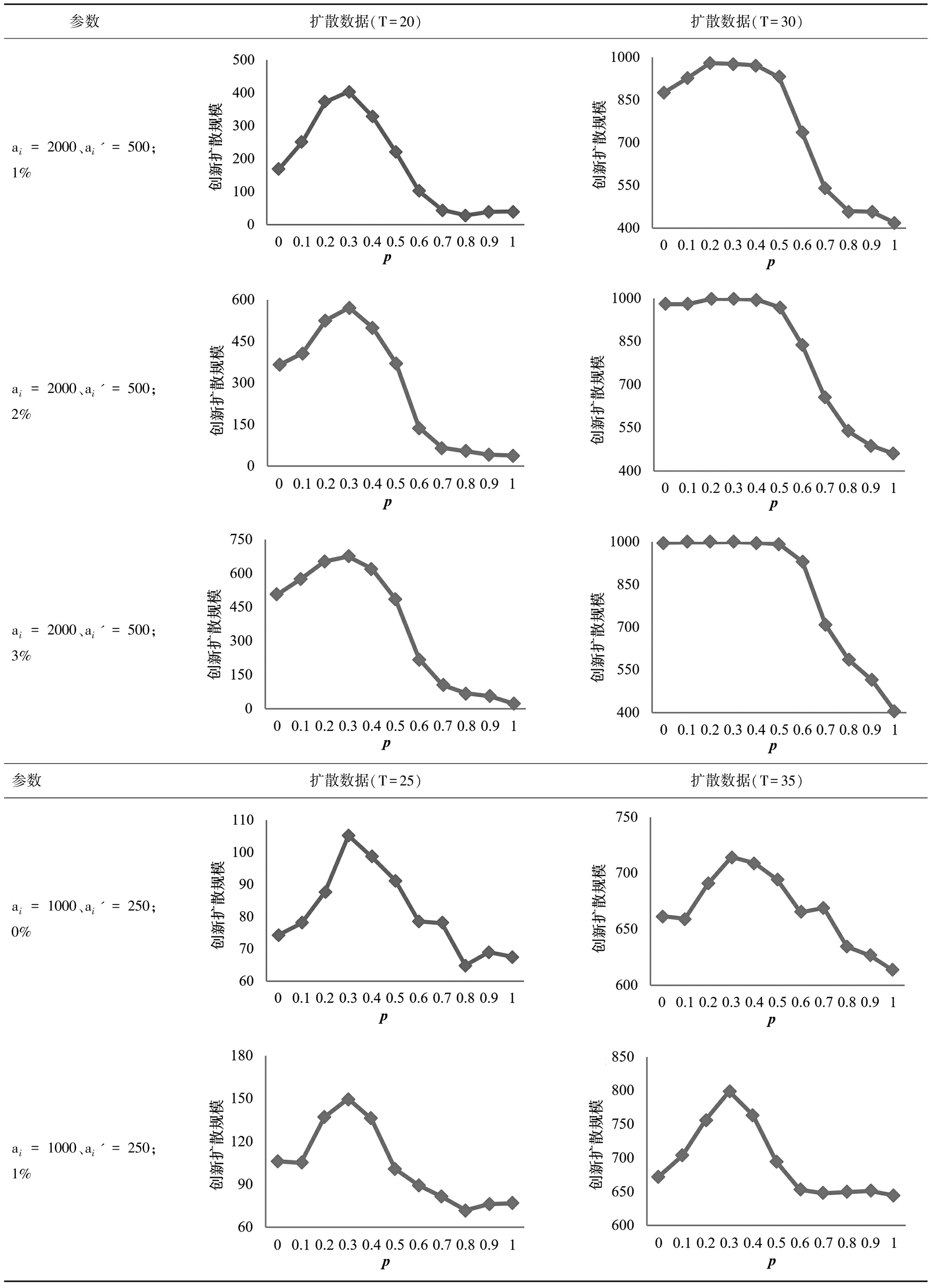
参数扩散数据(T=20)扩散数据(T=30)ai=2000、ai'=500;1%ai=2000、ai'=500;2%ai=2000、ai'=500;3%参数扩散数据(T=25)扩散数据(T=35)ai=1000、ai'=250;0%ai=1000、ai'=250;1%
续表1 不同参数组合下创新扩散数据
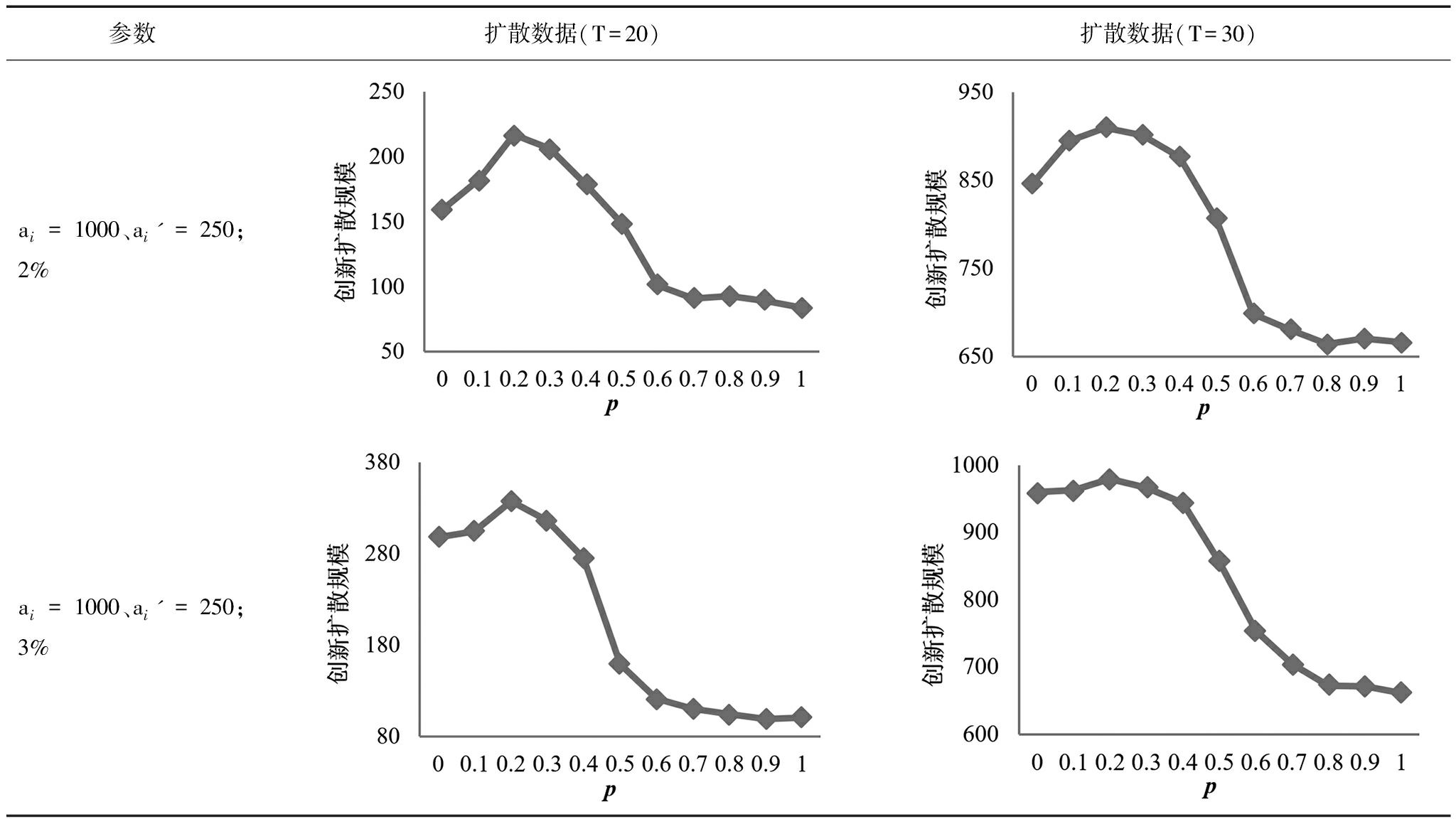
参数扩散数据(T=20)扩散数据(T=30)ai=1000、ai'=250;2%ai=1000、ai'=250;3%
不过,在0.3i=2 000、ai'=500时基本相同,并且,网络效应强度降低导致的不同p值下创新扩散规模的差距缩小。
为了检验创新先驱者比例提高对创新扩散规模的边际影响是否存在边际递减效应,分别计算高、低网络效应强度下,同样p值水平下创新先驱者比例每提高1%,创新扩散规模变化数据,见表2。
折线图显示,在网络效应强度较高的网络中,当p≤0.5时,在扩散的第20代和第30代,创新先驱者比例由0%增加到1%引起的扩散规模增加幅度最大,由2%增加到3%引起的扩散规模增加幅度最小,这说明创新先驱者比例提高对创新扩散规模促进作用随创新先驱者比例的增加而边际递减。不过,当p>0.5时,在不同的创新先驱者比例下,进一步提高创新先驱者比例对创新扩散规模的促进作用变得随机。在网络效应强度较低的网络中,当p≤0.5时,在扩散的第25代,创新先驱者比例由2%增加到3%对扩散规模促进作用最强;在第35代,当p≤0.5时,创新先驱者比例由1%增加到2%对创新扩散的促进作用最强。当p>0.5时,在第25代、第35代,在不同的创新先驱者比例下,进一步提高创新先驱者比例对创新扩散规模的促进作用都是随机的。数据结果部分支持了假设H3b。
表2 创新先驱者比例提高对创新扩散规模的促进作用分析
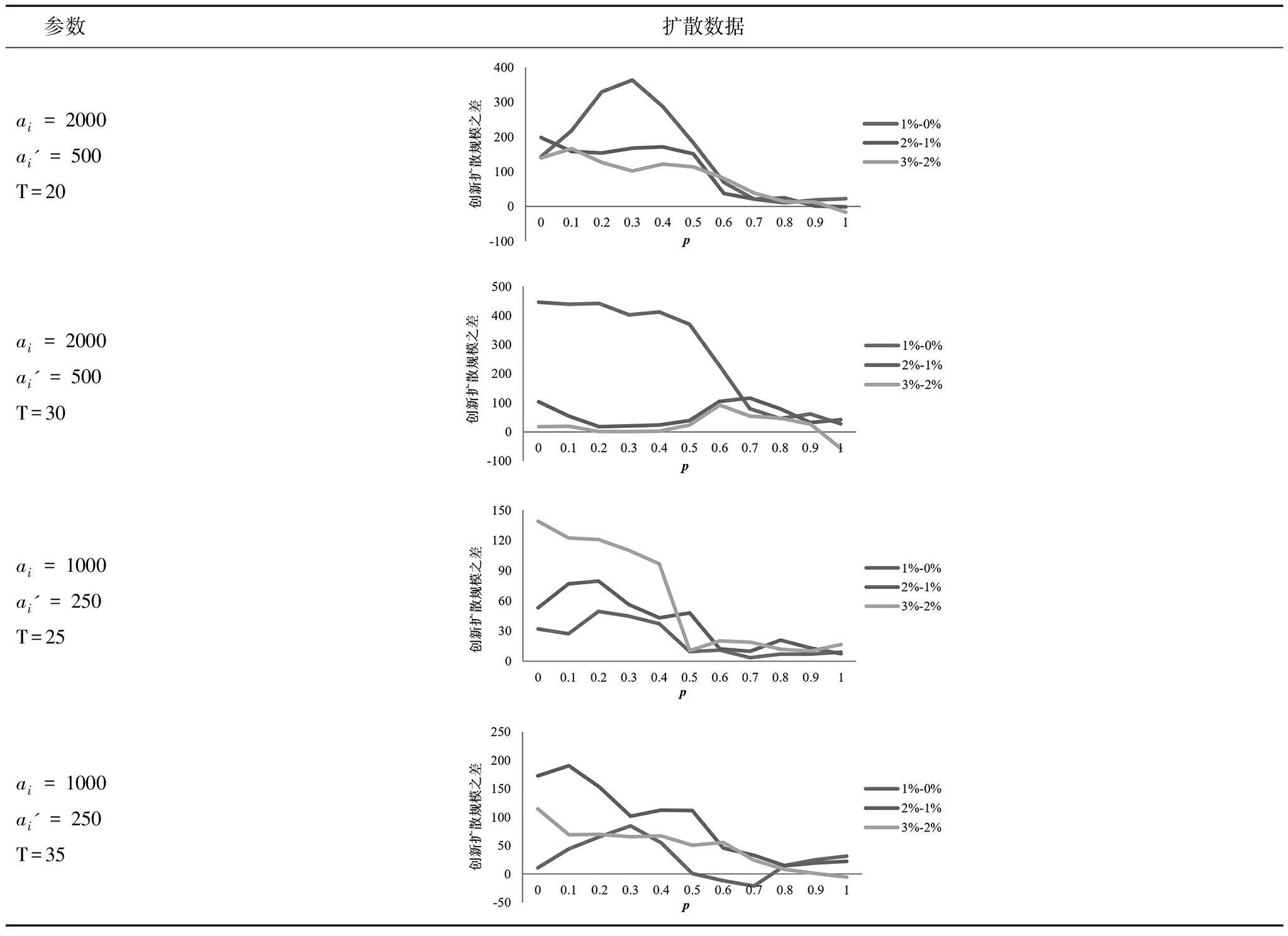
参数扩散数据ai=2000ai'=500T=20ai=2000ai'=500T=30ai=1000ai'=250T=25ai=1000ai'=250T=35
为了保证研究结论的稳健性,本文对单一扩散模型的关键参数,包括网络效应强度、初始技术绩效、技术吸收难度、采纳者偏好、创新先驱者比例等进行敏感性分析。结果显示,关键参数数值改变后并未使研究结论发生根本性变化,说明本文结论是稳健可靠的。
5 结论与启示
本文使用p-GNC网络拟合社交时代的个体网络,定量分析了网络结构、网络效应强度和社会系统中创新先驱者比例对创新扩散规模的影响,得出以下结论:①创新的市场扩散会依次经历起飞期、快速扩散期和稳定期;②p-GNC网络的平均聚集系数越大、平均度越小,创新扩散规模越大,且平均度是创新扩散规模的决定因素;③在p-GNC网络中,网络效应强度越高,创新扩散规模越大,网络结构变动对创新扩散规模的影响也越大;④在p-GNC网络中,创新先驱者比例越高,创新扩散规模越大。当网络效应强度较高且网络呈现出稀疏状态时,提高创新先驱者比例对创新扩散规模的促进作用随创新先驱者比例的增加而边际递减。
本文对创新扩散理论研究具有一定贡献。
(1)丰富了复杂网络模型在创新扩散研究中的应用。作为复杂网络模型发展的最新成果,p-GNC网络通过复制而实现动态增长的机制恰好能反映新社交环境下人与人之间通过微信、微博等社交平台的“好友推荐”功能而结识好友的好友,从而扩大人际网络的发展过程。并且,该网络具有强大的兼容性,仅需要调节复制概率的大小就可实现稀疏网络和稠密网络的转化。为此,本文将p-GNC网络引入创新扩散研究中,基于该网络进行创新扩散研究,得出了许多有价值的研究结论,丰富了复杂网络模型在创新扩散研究中的应用。
(2)从创新供给方和创新采纳方两方面构建创新扩散模型,为建立创新扩散模型提供了新思路。已有创新扩散模型往往简单地将创新内在效用视为外生的固定值或者随机变量,本文将创新供给方——企业也纳入扩散模型中,将企业层函数与个体效用函数相结合,为建立创新扩散模型提供了新思路。
(3)辨析了社会网络结构、网络效应强度和创新先驱者比例对创新扩散规模的影响,是对已有研究的有益补充。本研究分别在稀疏网络结构和稠密网络结构中分析了网络聚集程度和度数特征对创新扩散规模的影响,并进一步探讨了网络聚集程度和网络度数特征对创新扩散规模的综合影响效果,讨论视角和结论更全面。另外,已有的扩散模型大多将网络效应强度视为固定的外生变量,本研究定量分析了网络效应强度改变对创新扩散的影响,有助于对社会网络环境下创新扩散形成更完整的认知。最后,本研究还关注了创新先驱者比例对创新扩散规模的影响,包括绝对影响效应和相对影响效应,丰富了社会网络环境下创新扩散研究成果。
本研究具有一定实践意义。社交时代,人与人更紧密地联系在一起,个体在获取新产品信息和进行新产品采纳决策时受到所处人际网络的显著影响,而人际网络围绕社交平台重新聚合构建。借助社交平台,率先尝试新产品的创新先驱者对新产品后期市场表现的影响也明显增强,这为企业实施新产品市场定位和营销带来了新挑战。基于这样的现实情境,本研究使用最贴近社交时代人际网络结构特性的p-GNC网络拟合创新采纳者网络,发现创新在p-GNC网络中的扩散规模存在明显周期性,企业可根据周期曲线分阶段施策。在扩散起飞期,企业应借助电视、报纸、社交平台等广泛宣传新产品,提高产品知名度,并通过低价吸引消费者尝试新产品;进入快速扩散期后,企业要扩大生产,提高新产品质量和技术含量,营销重心从宣传创新转移到建立口碑和声誉上;当创新扩散到达稳定期,企业要节省成本,审慎评估创新,改良具有发展潜力的创新,放弃潜力不足的创新。另外,研究还表明,在平均度越小、平均聚集系数越大且网络效应越强的网络中,创新产品扩散规模越大,且网络效应越强,网络结构变动对创新扩散规模的影响越大。这启示企业在选择新产品目标客户群时,应着重争取那些朋友圈子比较小、集团化程度比较高、朋友之间相互影响程度比较大的客户。对于手机、软件等网络效应很强的创新产品,客户群体结构对新产品销量的影响会远远高于日用品、药品等网络效应较弱的创新产品,前者在选择目标客户群体时需要尤其谨慎,并且在新产品推广过程中要高度关注客户群体结构变动情况。最后,研究显示,在p-GNC网络中,创新先驱者比例越高,创新扩散规模越大。因此,在进行新产品前期推广时,应选择年轻白领、大学生等创新先驱者比较多的群体,并借助社交网络营销、体验营销等时尚营销方式,尽可能争取到创新先驱者的青睐。
参考文献:
[1] CHOI H,KIM S H,LEE J.Role of network structure and network effects in diffusion of innovations[J].Industrial Marketing Management,2010,39(1):170-177.
[2] 曹霞,张路蓬,刘国巍.基于社会网络结构的创新扩散动力机制及其仿真研究[J].运筹与管理,2018(5):149-156.
[3] DOROGOVTSEV S N,MENDES J F F.Scaling properties of scale-free evolving networks:continuous approach[J].Physical Review E,2001,63(5).
[4] AHN Y Y,HAN S,KWAK H,et al.Analysis of topological characteristics of huge online socialnetworking services[C].Proceedings of the 16th International Conference on World Wide Web,ACM,2007:835-844.
[5] ZHANG G Q,ZHANG G Q,YANG Q F,et al.Evolution of the Internet and its cores[J].New Journal of Physics,2008,10(12).
[6] WATTS DJ.Small worlds:the dynamics of networks between order and randomness[J].Physics Today,2007,31(6):74-75.
[7] CENTOLA D,EGU LUZ V M,MACY M W.Cascade dynamics of complex propagation[J].Physica a Statistical Mechanics & its Applications,2007,374(7):449-456.
LUZ V M,MACY M W.Cascade dynamics of complex propagation[J].Physica a Statistical Mechanics & its Applications,2007,374(7):449-456.
[8] 黄玮强,姚爽,庄新田,等.基于无标度网络的创新扩散模型研究[J].东北大学学报(自然科学版),2015,36(8):1212-1216.
[9] KATZ M L,SHAPIRO C.Network externalities,competition and compatibility[J].The American Economic Review,1985,75(3):424-440.
[10] IRWIN E G,BOCKSTAEL N E.Interacting agents,spatial externalities and the evolution of residential land use patterns[J].Journal of Economic Geography,2002,2(1):31-54.
[11] 孙军,高彦彦.网络效应下的平台竞争及其后果分析[J].管理世界,2016(5):182-183.
[12] 周琦萍,徐迪,杨芳.基于复杂社会网络和局部网络效应的新产品竞争扩散的计算实验研究[J].软科学,2013,27(7):13-17.
[13] MOORE C,NEWMAN M E J.Epidemics and percolation in small-world networks[J].Physical Review E,2000,61(5):5678-5682.
[14] PASTOR-SATORRAS R,VESPIGNANI A.Epidemic spreading in scale-free networks[J].Physical Review Letters,2001,86(14):3200-3203.
[15] UYAR A,KARACA Y.Influence of opinion leaders on the diffusion of innovative products:a study on smart-phone users[J].Journal of Business Economics & Finance,2014,3(2):233-246.
[16] 陈涛,付欢.社会网络环境下意见领袖对消费者创新抗拒的影响研究[J].工业技术经济,2014(8):58-66.
[17] 赵新刚,闫耀民,郭树东.企业产品创新的扩散与采纳者的行为决策模式研究[J].中国管理科学,2006,14(5):98-103.
[18] IYENGAR R,VAN DEN BULTE C,VALENTE T W.Opinion leadership and social contagionin new product diffusion[J].Marketing Science,2011,30(2):195-212.
[19] ZHAO Y,KOU G,PENG Y,et al.Understanding influence power of opinion leaders in e-commerce networks:an opinion dynamics theory perspective[J].Information Science,2018,426:131-147.
[20] ROGERS E M.Diffusion of innovations[M].New York:Free Press,1983.
[21] BHAT U,KRAPIVSKY P L,LAMBIOTTE R,et al.Densification and structural transitions in networks that grow by node copying[J].Physical Review E,2016,94(6-1).
[22] 黄玮强,庄新田.网络结构与创新扩散研究[J].科学学研究,2007,25(5):1018-1024.
[23] PEGORETTI G,RENTOCCHINI F,MARZETTI G V.An agent-based model of innovation diffusion:network structure and coexistence under different information regimes[J].Journal of Economic Interaction & Coordination,2012,7(2):145-165.
[24] 黄玮强,庄新田,姚爽.网络外部性条件下新产品扩散的赠样策略研究[J].管理科学学报,2009,12(4):51-63.
[25] CENTOLA D.The social origins of networks and diffusion[J].American Journal of Sociology,2015,120(5):1295-1298.
[26] 林略,周力全.小世界网络下用户创新扩散效果分析[J].技术经济,2009,28(7):18-21.
[27] CENTOLA D.The spread of behavior in an online social network experiment[J].Science,2010,329(5996):1194-1197.
[28] 黄玮强,庄新田.基于随机网络的创新扩散研究[J].管理学报,2007,4(5):622-627.
[29] 娄思源.基于社会网络的创新扩散仿真研究[D].杭州:浙江大学,2012.
[30] 徐翔斌,李恒,王坤.Web2.0网络信息传播影响机制研究[J].情报科学,2015(8):44-49.
[31] 毛艳.基于创新扩散理论的微信信息传播机制研究[D].上海:上海工程技术大学,2016.
[32] 郑木华.复杂网络上复发式流行病爆发的研究[D].上海:华东师范大学,2017.
[33] LEE E,LEE J,LEE J.Reconsideration of the winner-take-all hypothesis:complex networks and local bias[J].Management Science,2006,52(12):1838-1848.
[34] 赵良杰,武邦涛,段文奇,等.消费者交互作用对网络效应产品扩散的影响——基于产品生命周期的视角[J].系统工程理论与实践,2012,32(1):67-75.
[35] 李凡.基于免费商品赠送的网络效应产品扩散研究[D].西安:西安工业大学,2011.
[36] 杨珊珊.跟风效应和网络效应影响下的数字信息产品扩散:复杂网络的视角[D].厦门:厦门大学,2014.
[37] TRUONG Y.A cross-country study of consumer innovativeness and technological service innovation[J].Journal of Retailing & Consumer Services,2013,20(1):130-137.
[38] 高键,盛光华,周蕾.绿色产品购买意向的影响机制:基于消费者创新性视角[J].广东财经大学学报,2016,31(2):33-42.
[39] ZUBCSEK P P,SARVARY M.Advertising to a social network[J].Quantitative Marketing & Economics,2011,9(1):71-107.
[40] 张磊.基于种子顾客权重网络的随机阈值模型研究[D].北京:北京邮电大学,2012.
[41] SCHUMPETER J.Capitalism,socialism,and democracy[J].New York:Harper and Row,1942.
[42] LEE J,LEE J,LEE H.Exploration and exploitation in the presence of network externalities[J].Management Science,2003,49(4):553-570.
[43] COHEN W M,LEVINTHAL D A.Innovation and learning:the two faces of R&D[J].The Economic Journal,1989,99(397):569-596.
(责任编辑:万贤贤)









 LUZ V M,MACY M W.Cascade dynamics of complex propagation[J].Physica a Statistical Mechanics & its Applications,2007,374(7):449-456.
LUZ V M,MACY M W.Cascade dynamics of complex propagation[J].Physica a Statistical Mechanics & its Applications,2007,374(7):449-456.