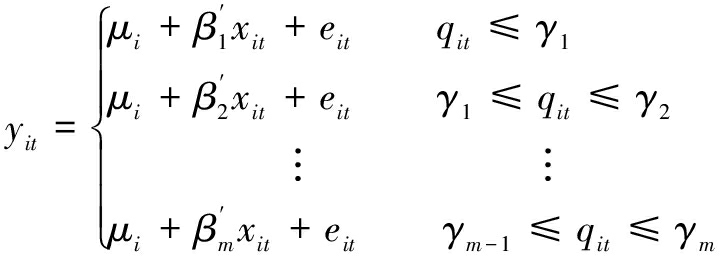
2017年，我国研发经费支出达到17 500亿元，占国内生产总值的比重为2.12%，同比增长11.6%。同年，我国创新指数提升至全球第17位，但与创新型国家如美国、日本和德国等相比仍存在较大差距，主要体现在企业创新能力不足等方面。
对企业而言，产品研发与技术创新的根本目的在于提升企业绩效。与一般要素投入不同，研发投入是一项高风险的投资活动，并且具有明显的阶段特征，即处于不同研发阶段的投资并不能确保等量资本获得等量收益。此外，研发投入对企业绩效的影响可能因创新速度的不同而不同(何佳、曾勇，2003；俞立平、 孙建红，2017)。现有研究大多将创新速度理解为时间维度，即将企业产品从研发到批量化生产或面世的时间跨度作为创新速度的度量依据，没有考虑到企业创新相对于行业其它企业所处的地位，忽略了行业竞争这一重要因素。处于行业创新领先地位的企业，享有研发先发优势，能够获得可观的垄断报酬。在当前经济转型升级提速的背景下，只有准确且全面把握研发投入对企业绩效提升的影响机制，才能有针对性地提出合理、有效的科技政策和研发策略。
本文将企业创新速度作为行业内相对研发强度，对2010—2016年我国A股上市公司研发强度、创新速度与上市公司价值之间的非线性关系进行实证研究。为了避免人为划分创新速度带来的偏误，本文基于面板门限回归模型，研究不同创新速度调节下研发强度与上市公司价值之间的关系。
长期以来，关于研发投入与企业绩效间关系的探讨一直是学术界关注的热点问题。企业绩效分为会计绩效和市场绩效两类。其中，会计绩效一般采用资产收益率、全要素生产率、股东权益回报率、每股收益等指标度量，主要反映企业历史经营成果；市场绩效一般采用托宾Q指标度量[1]。
大量研究表明，研发投入可能存在边际效率递减规律，当超过某个临界值时，研发投入就不会再产生等比例的投资回报，即二者之间可能不仅仅是简单的线性关联。例如，戴小勇和成力为(2013)基于我国工业企业数据，借助面板门限回归模型，从全要素生产率和资产收益率两个方面对企业绩效进行度量，研究了研发投入对企业绩效的非线性影响，发现研发投入与企业绩效之间存在双门限关系，只有研发投入达到第一门限值时才会对企业绩效产生显著影响；超过第二门限值时，对企业绩效的作用不再明显，并且这种影响存在行业差异。陈建丽等(2015)基于我国计算机、通信和其它电子设备制造业上市公司数据，选取营业利润率作为企业绩效的代理指标，运用面板门限回归模型，对研发投入和企业绩效的关系进行了研究，发现研发投入与企业绩效间存在双门限效应。韩先锋和惠宁(2016)运用面板门限回归方法，选取研发投入作为门限变量，考察了研发投入对不同所有制战略性新兴产业企业绩效的非线性影响，研究发现所有制差异视角下研发投入与战略性新兴企业绩效之间存在显著的异质非线性关系。韩先锋和董明放(2018)同样运用面板门限回归方法，分别选取研发投入、企业规模、资本密度和资本结构等指标作为门限变量，探讨了研发投入对我国智慧城市企业绩效的异质门限效应，发现研发投入对企业绩效具有非线性影响。区别于上述研究，项云帆[1]从企业市场绩效视角出发，探讨了研发强度是否对上市公司价值存在影响，研究表明研发强度对上市公司价值具有门限效应，即随着研发强度由小到大，其对上市公司价值的影响由负向到不显著再到正向。在此基础上，项云帆[2]运用中国上市公司面板数据，通过构建解释变量平方项的方法，探究了创新投入、创新速度及技术商品化导向的投入对企业会计绩效和市场绩效的影响，研究发现创新投入对企业会计绩效和市场绩效均具有显著非线性效应。
以上研究对研发投入与企业绩效之间的关系进行了探索，丰富了学术界对二者关系的研究，为我国政府和企业制定科技政策、研发策略提供了可信的经验证据，但大多数研究聚焦于企业自身研发投入与其绩效之间的非线性关系探讨上，未考虑行业竞争因素对二者之间非线性关系的影响。事实上，行业内企业往往竞争激烈，研发及创新领先会给企业带来先发优势，如持续的竞争力维持以及产品生命周期改善等，从而更快速地转化为生产力，获取垄断报酬。Stalk[3]首次提出“基于时间竞争”的概念，认为快速创新可以提升企业的时间竞争优势。在该理论支撑下，国外学者将技术创新速度概括为从创新想法诞生到产品生产并推向市场所花费的时间，并广泛运用于研究中[4,5]。国内学者关于创新速度的研究相对较少，且大多将创新速度定义为一个时间概念 (夏晖、曾勇，2005；宋浩亮，2010；吴爱华、苏敬勤，2012)。这种用时间度量创新速度的方式存在以下不足：第一，缺乏对行业内部竞争因素的考量。一味追求新产品快速投放市场，单纯考虑时间花费而不考虑同行业研发强度水平，并不能达到以创新提升绩效的预期；第二，与当前产品创新理念以及国家政策导向存在偏差。企业一味缩短创新时间可能带来产品品质低劣、市场反应不佳等问题，与国家追求产品质量提升的导向背离；第三，忽略了当前企业创新活动的新趋势、新变化。“众创意”等开放式创新社区的产生改变了原有的创新研发模式，创新活动由依靠企业内部逐渐转变成依靠创客群体[6]。创客群体创新思维产生时间具有不确定性，单纯用创意产生到产品面世的时间跨度衡量创新速度有其局限性。
本文在Garner等[7]及项云帆[1]研究的基础上，用公司自身研发强度与同行业所有公司平均研发强度的比重作为创新速度的代理变量，选取上市公司价值为被解释变量、研发强度为解释变量、创新速度为门限变量，对2010-2016年我国A股上市公司研发强度、创新速度与上市公司价值之间的非线性关系进行实证研究。本文创新之处主要体现在：第一，着重探究研发强度与上市公司价值之间的关系。已有研究大多关注企业会计绩效，对上市公司价值的关注度欠缺。本文致力于研究二者之间的作用机制，为我国上市公司研发创新激励提供政策参考；第二，充分考虑行业竞争加剧、产品思维转变以及创新途径多样化的新趋势，采纳反映行业内部竞争状况的指标代理创新速度。这种基于相对数的创新速度衡量指标更加关注同行业竞争状况，跳出了一味追求快速创新的桎梏，符合当前创新发展趋势；第三，优化研发强度对上市公司价值门限效应的研究思路，通过引入创新速度指标作为门限变量，进一步丰富和完善实证分析过程。
门限模型最早是由Tong[8]，Tong & Lim[9]提出的一类非线性计量经济模型，在自然科学和社会科学等多个领域应用广泛。门限模型通过假设经济系统各变量在不同区制下服从不同线性关系来描述复杂的非线性现象，适用于经济系统中存在两个或者多个区制，且经济系统各变量之间的关系在不同区制间跳跃变化的情形。门限模型的区制转换机制由可观测门限变量和门限值决定。具体来说，当门限变量观测值超过某个门限值时，经济系统各变量之间的关系将从一个区制转换到另一个区制。这种区制转换机制使得门限模型具有估计方法简单及经济解释直观的优点。
门限模型的门限值由模型内生决定。根据门限值个数，门限模型可以分为两类：单门限模型和多门限模型。Hansen[10]首次构建了适用于平衡面板数据的面板门限回归模型，并提出了相应的估计和检验方法。具体而言，给定面板数据yit,qit,xit:1≤i≤n,1≤t≤T，包含m个区制的多门限模型的数学表达式为：
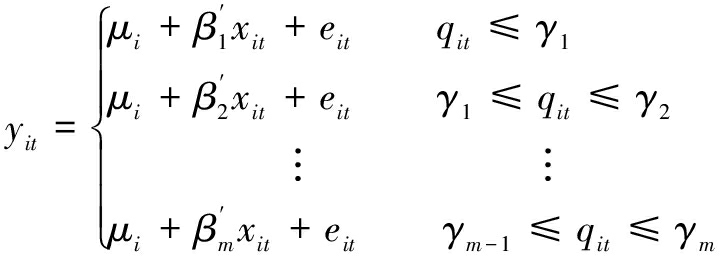
(1)
其中，i表示个体；t表示时期；m表示区制个数；yit表示被解释变量；xit表示k×1维解释变量；qit表示门限变量；μi表示个体效应；eit表示服从均值为0，方差为σ2的独立同分布随机变量；γj=(j=1,2,…,m)表示门限值；βj=(j=1,2,…,m)表示第j个区制的回归系数。
对于单门限模型，其表达式为：
(2)
其中，I(·)表示示性函数，取值为0或者1。针对上述单门限模型，可采用Chan[11]提出的剖面最小二乘(Profile Least Square，PLS)估计方法对其进行估计。具体估计步骤如下：①将门限变量取值从低到高排序，确定可取的门限值序列；②依次假定门限值序列中的元素为门限值，将所研究的变量进行分组，对每个分组进行线性回归，计算得到回归系数的条件最小二乘估计量
和
为了确保在每个区制都有适当数量的观测值，一般假定每个区制所包含的数据量不低于观测值总数的一定比例，如1%或者5%；③通过最小化门限模型的残差平方和S1(γ)，即可得到门限值的估计值
④基于门限值的估计值
进一步得到回归系数的估计值
和
在门限模型中，有一类非常重要的假设检验，即判断门限模型是否存在门限效应。实际分析中，如果没有特别令人信服的非线性证据，学者们研究分析的首要选择仍然是形式和估计方法都很简单的线性模型。门限效应的检验恰恰为是否应该使用门限模型提供了严格的理论证据。
门限效应检验所对应的原假设和备则假设分别为：H0∶β1=β2,H1∶β1≠β2，其检验统计量为：
(3)
其中，S0表示线性模型的残差平方和，
和
分别表示单门限模型的残差项平方和、残差项方差估计值。当原假设H0∶β1=β2成立时，门限值γ将成为冗余参数或者不可识别参数，因此上述检验统计量在原假设下的渐进分布不再为标准卡方分布。Hansen[12]首次提出采用自举法(Bootstrap)计算得到上述F检验统计量的临界值和p值，大大简化了门限效应的检验难度，为门限模型提供了一种便捷有效的检验方法。如果门限效应检验证实模型中存在门限效应，即β1≠β2，则还需进一步对门限真值进行检验，即检验门限值的估计值是否为门限真值。门限真值检验所对应的原假设和备则假设分别为H0∶γ=γ0,H1∶γ≠γ0，检验统计量为：
(4)
该检验统计量在原假设下的渐进分布仍为非标准分布。Hansen[10]给出了一个计算上述LR检验统计量临界值(上α分位数)的计算公式，即
为显著性水平。根据临界值，可以得到门限估计值的置信区间。
在大多数实证应用中，可能存在多个门限值。以双门限模型为例，其模型表达式为：
(5)
其中，γ1<γ2。针对在运用PLS估计方法时双门限模型计算量过大的问题，Hansen[10]建议采用序贯估计方法对双门限模型进行估计。具体步骤为：第一阶段，对单门限模型进行估计，得到第一个门限值的估计量
第二阶段，假设第一阶段门限值的估计值
已知，通过最小化门限模型的残差平方和：
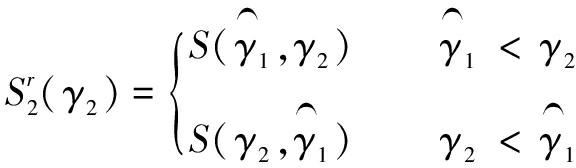
(6)
得到第二个门限值的估计量
Bai[13]证明
是渐进有效的，而则非渐进有效。对于
由于估计时忽略了其它区制的存在，需对其进行进一步修正；第三阶段，假设第二阶段门限值估计值已知，通过最小化门限模型的残差平方和：
(7)
得到第一个门限值的估计量
与单门限模型不同的是，双门限模型除需要判断模型是否为线性模型外，还需在存在门限效应的前提下进一步对门限值的个数进行检验。门限值个数检验所对应的原假设和备则假设分别为：H0只有1个门限值，H1至少存在2个门限值，其检验统计量为：
(8)
其中，
表示存在2个门限值时的残差项方差估计值。类似地，可以采用自举法(Bootstrap)计算得到上述F检验统计量的临界值和p值。对于双门限模型，与单门限模型相似，门限真值的检验统计量为：
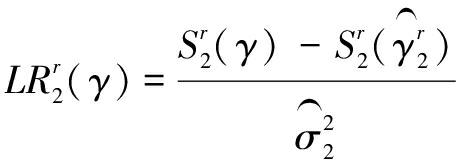
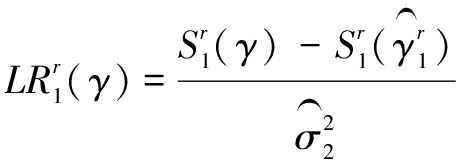
(9)
根据LR检验统计量临界值(上α分位数)计算公式，可以进一步得到门限估计值置信区间。对于3个或者多个门限值的情形，其估计和检验方法与上述方法类似，不再赘述。
本文以在上海和深圳证券交易所上市的所有A股上市公司为研究对象，数据来源于Wind金融数据库和国泰安(CSMAR)数据库。本文所采用的数据为面板数据，年限跨度选择依据如下：①考虑到2010年前披露研发费用数据的上市公司样本较少，而本文研究方法仅适用于平衡面板数据，为保证面板数据所涉及的样本量足够充分，本文选择2010年后的数据；②考虑到2017年科技型中小企业研发费用加计扣除的比例提高且范围扩大，导致研发费用统计口径存在差异，为了确保数据的连续性和一致性，排除税收政策的外部性影响，本文样本区间设定为2010—2016年。剔除存在数据缺失的公司个体后，得到符合样本要求的819家公司，共计5 733个样本。
本文选取上市公司价值为被解释变量、研发强度为核心解释变量、创新速度为门限变量，资产结构、公司规模、市净率、资产负债率、流动比率、股权集中度等变量为控制变量，对研发强度、创新速度与上市公司价值之间的非线性关系进行实证研究。具体变量设定如下：
(1)被解释变量。本文采用托宾Q(Tobin'sQ)作为上市公司价值的代理变量。托宾Q是上市公司的金融市场价值(包括公司股票市值和债务资本的市场价值)对其资产重置成本的比率，可以反映公司成长机会，其数值越高，成长机会越大，公司价值越高。由于我国资产重置成本和非流通股市值数据不可获得，文献中一般采用公司总资产的账面价值替代重置成本。本文托宾Q的计算公式如下所示：
(10)
其中，CAPit表示公司i在t年份的金融市场价值，具体计算方式为：(总股数—境内上市的外资股B股)×今收盘价A股当期值+境内上市的外资股B股×今收盘价当期值×当日汇率+负债合计本期期末值；TAit表示公司i在年份t的总资产。
(2)核心解释变量。本文采用研发强度(RDI)作为核心解释变量。在现有关于研发投入的研究中，广泛使用研发强度衡量研发投入。一般而言，大规模公司(如蓝筹股公司)相比小规模公司(如创业板公司)，拥有更为充沛的资产和现金流储备，在研发费用上可供周转的资金更多。为了有效剔除公司规模因素对研发费用的影响，本文参考Lin等[14]和项云帆[1,2]的研究，采用研发费用占公司总资产的比重度量研发强度，该数值越大，表明上市公司的研发强度越高。相比研发费用指标，研发强度可以对不同规模公司研发投入程度的大小进行合理对比。本文研发强度计算公式为：
(11)
其中，RDit表示公司i在年份t的研发费用总和。
(3)门限变量。本文参考Garner等[7]和项云帆[1]的做法，将公司自身研发强度与同行业所有公司平均研发强度的比重作为创新速度(INS)的代理变量，具体计算公式为：
(12)
其中，ARDindustryi,t表示公司i在年份t所属行业的平均研发费用；ATAindustryi,t表示公司i在年份t所属行业的平均总资产。
(4)控制变量。为了得到可靠的研究结论，本文对可能影响公司价值的其它变量进行控制，具体包括：资产结构、公司规模、市净率、资产负债率、流动比率和股权集中度等6个变量。
资产结构(AS)：各类资产占公司总资产的比重，是企业内部资源配置的表现形式，其计算公式为：
(13)
其中，FAit表示公司i在年份t的固定资产总额；Iit表示公司i在年份t的存货总额。
公司规模(SIZE)：一定程度上决定了公司现金流充裕程度，不同规模公司在研发投入、生产运作和市场营销等直接影响公司价值的经营活动上存在较大差异。本文用总资产的自然对数衡量公司规模，即：
SIZEit=lnTAit
(14)
市净率(PB)：每股股价与每股净资产的比率，反映公司的成长机会，常用于股票估值，计算公式为：
(15)
其中，SPit表示公司i在年份t的每股股价，BVPSit表示公司i在年份t的每股净资产。
资产负债率(DAR)：又称杠杆率，即企业负债总额和资产总额的比重，是资本结构的主要代理变量，其计算公式为：
(16)
其中，TDit表示公司i在年份t的负债总额。
流动比率(CR)：流动资产对流动负债的比率，用来衡量企业流动资产在短期债务到期以前可以变为现金用于偿还负债的能力，其计算公式为：
(17)
其中，CLit表示公司i在年份t的流动负债，CAit表示公司i在年份t的流动资产。
股权集中度(SCR)：全部股东因持股比例不同所造成的股权集中或分散的数量。考虑到股权集中度对公司价值可能存在影响，本文将股权集中度作为控制变量，并用公司前五大股东持股比例的平方和对其进行度量，具体计算公式为：
(18)
其中，INSTQi,jt表示公司i在年份t第j大股东的持股比例。
表1变量描述统计量
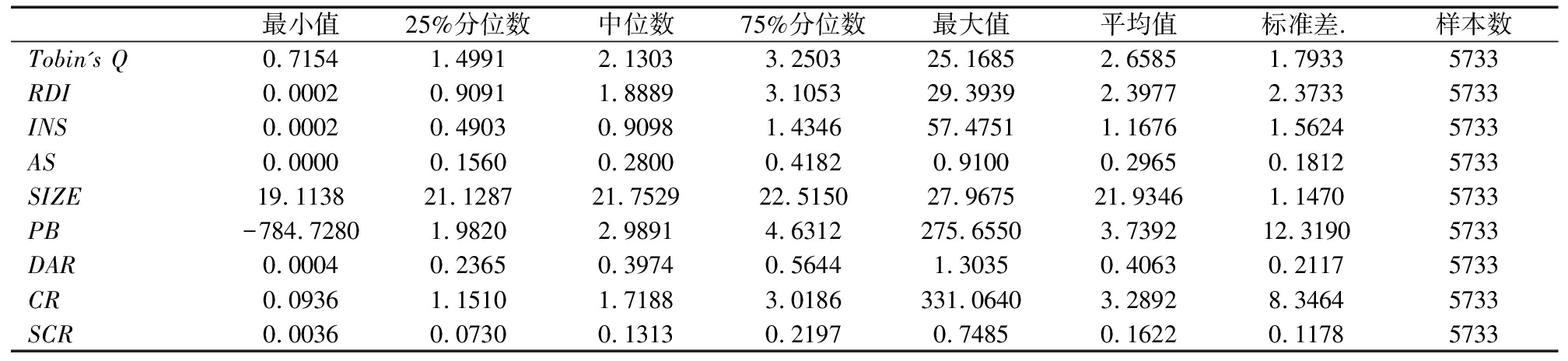
最小值25%分位数中位数75%分位数最大值平均值标准差.样本数Tobin's Q0.71541.49912.13033.250325.16852.65851.79335733RDI0.00020.90911.88893.105329.39392.39772.37335733INS0.00020.49030.90981.434657.47511.16761.56245733AS0.00000.15600.28000.41820.91000.29650.18125733SIZE19.113821.128721.752922.515027.967521.93461.14705733PB-784.72801.98202.98914.6312275.65503.739212.31905733DAR0.00040.23650.39740.56441.30350.40630.21175733CR0.09361.15101.71883.0186331.06403.28928.34645733SCR0.00360.07300.13130.21970.74850.16220.11785733
表2单位根检验结果
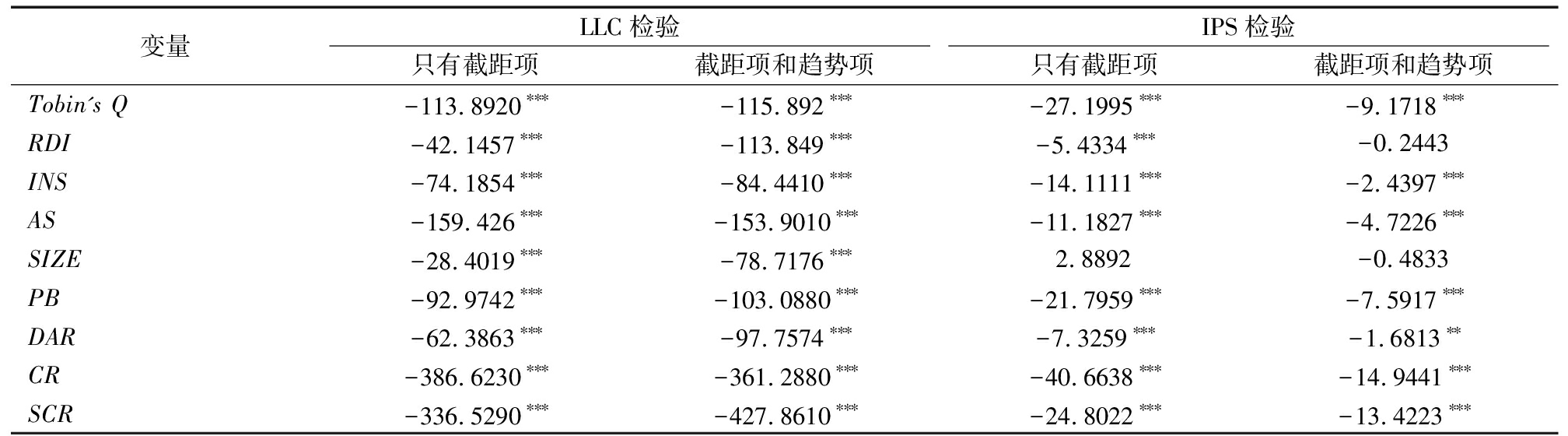
变量LLC检验IPS检验只有截距项截距项和趋势项只有截距项截距项和趋势项Tobin's Q-113.8920∗∗∗-115.892∗∗∗-27.1995∗∗∗-9.1718∗∗∗RDI-42.1457∗∗∗-113.849∗∗∗-5.4334∗∗∗-0.2443INS-74.1854∗∗∗-84.4410∗∗∗-14.1111∗∗∗-2.4397∗∗∗AS-159.426∗∗∗-153.9010∗∗∗-11.1827∗∗∗-4.7226∗∗∗SIZE-28.4019∗∗∗-78.7176∗∗∗2.8892-0.4833PB-92.9742∗∗∗-103.0880∗∗∗-21.7959∗∗∗-7.5917∗∗∗DAR-62.3863∗∗∗-97.7574∗∗∗-7.3259∗∗∗-1.6813∗∗CR-386.6230∗∗∗-361.2880∗∗∗-40.6638∗∗∗-14.9441∗∗∗SCR-336.5290∗∗∗-427.8610∗∗∗-24.8022∗∗∗-13.4223∗∗∗
注：单位根检验的原假设为存在同质(异质)单位根；备则假设为不存在单位根；***、**、*分别表示通过1%、5%、10%水平显著性检验；下同
由表1可知，Tobin'sQ的平均值为2.658 5，标准差为1.793 3，极差(最大值减去最小值)为25.453 1，可见我国不同上市公司价值差距悬殊。RDI的标准差为2.373 3，极差为29.393 7；INS的标准差为1.167 6，极差为57.474 9，表明我国上市公司在研发投入和创新速度方面两极分化严重，部分企业以研发创新为价值增长点，部分企业缺乏创新活力。
为了避免伪回归现象，面板门限回归模型中要求门限变量为平稳变量，同时由于数据的非平稳可能导致回归结果偏差，本文分别采用同质单位根的LLC(Levin-Lin-Chu)检验[15]和异质单位根的IPS(Im-Pesaran-Skin)检验[16]对模型中的变量进行面板单位根检验，考虑只含截距项与同时包含截距项和趋势项两种检验情形，面板数据单位根检验结果如表2所示。除极个别IPS检验结果不显著外，其余面板数据单位根检验结果均显著拒绝原假设，接受不存在单位根的备则假设，说明本文选取的变量均为平稳变量，不存在伪回归问题，可以进行面板回归分析。
在采用面板门限回归模型前，首先需要对是否存在门限效应以及存在几重门限效应进行检验，以便准确识别研究方法的合理性，并且判断门限模型的具体形式和门限值个数。本文借助Hansen[12]提出的Bootstrap方法依次对单门限值、双门限值和三门限值的存在性进行检验，原假设分别为没有门限值、只有1个门限值、只有2个门限值。模型估计后，通过300次Bootstrap模拟计算得到门限效应F检验统计量的临界值和p值。
表3门限效应检验
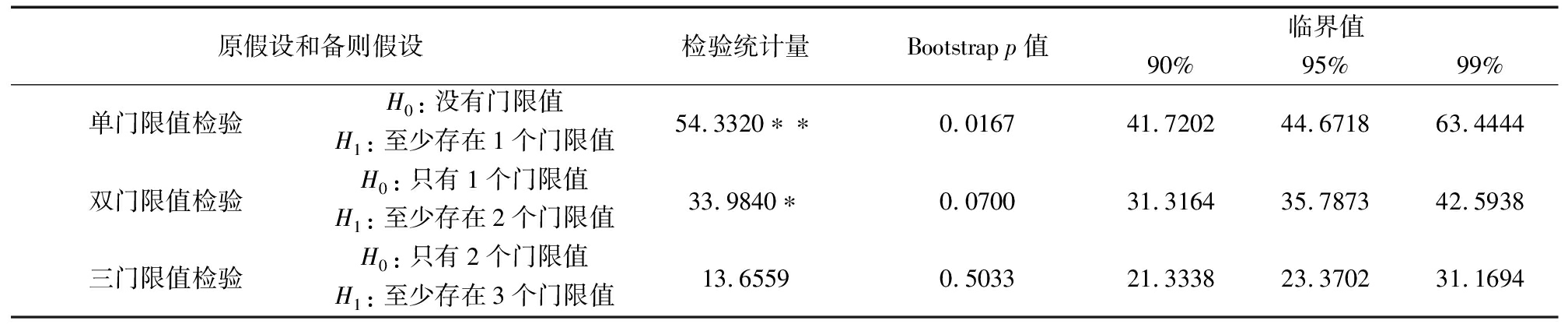
原假设和备则假设检验统计量Bootstrap p值临界值90%95%99%单门限值检验H0:没有门限值H1:至少存在1个门限值54.3320∗∗0.016741.720244.671863.4444双门限值检验H0:只有1个门限值H1:至少存在2个门限值33.9840∗0.070031.316435.787342.5938三门限值检验H0:只有2个门限值H1:至少存在3个门限值13.65590.503321.333823.370231.1694
由表3可知，在单门限值检验中，得到F统计量为54.332 0，计算出相应的Bootstrapp值为0.016 7，在5%的显著性水平下拒绝了没有门限值的假设，说明至少存在一个门限值。在此基础上的双门限值检验发现，F统计量为33.984 0，相应的Bootstrapp值为0.070 0，在10%的显著性水平下拒绝了只存在1个门限值的假设，说明至少存在2个门限值。当进行三门限值检验时，F统计量值为13.655 9，相应的p值为0.503 3，检验结果接受原假设，说明只有2个门限值。由于单一门限和双重门限效应显著，而三重门限效应不显著，据此本文选择双门限模型探讨研发强度、创新速度与上市公司价值之间的关系。
基于本文所选研究变量在完成门限效应检验后，需要进一步对双门限模型的门限值进行估计及检验，利用Hansen[10]中多门限模型估计方法，可以得到门限估计值及其置信区间。表4为门限估计值及其在95%置信水平下的置信区间。可知，双门限模型的第一门限估计值是1.153 3，其95%置信区间是[1.141 3,1.278 2]；第二门限估计值是2.649 6，其95%置信区间是[2.583 7,2.784 3]。
表4门限估计值与置信区间
估计值95%置信区间第一门限值1.153 3[1.141 3, 1.278 2]第二门限值2.649 6[2.583 7, 2.784 3]
借助门限真值的LR检验统计量，可以对门限估计值是否等于其真实值进行检验。图1、2为不同门限取值情形下LR检验统计量的函数图，其中横轴表示门限值，纵轴表示LR检验统计量值。图1和图2中，门限估计值是LR检验统计量值为0时门限值的取值。LR检验统计量在95%置信水平下的临界值在图中用虚线表示。LR检验统计量值在虚线以下部分所对应的门限值所在区间即为门限估计量在95%置信水平下的置信区间。
本文重点分析研发强度与上市公司价值之间的关系。为了对比研发强度对上市公司价值的线性影响和非线性影响，本文分别采用面板线性回归模型和面板门限回归模型对我国2010-2016年819家A股上市公司的数据进行估计。在面板门限回归模型中，本文以公司自身研发强度与同行业所有公司平均研发强度的相对数定义的创新速度作为门限变量。在上文门限值估计与检验中，本文得到的两个门限值分别是1.153 3和2.646 9。根据创新速度和门限值，可以将研发强度对上市公司价值的影响划分为3个不同区制。具体而言，区制1表示创新速度处于“慢车道”(INS≤1.153 3)；区制2表示创新速度处于“正常行车道”(1.153 3<INS≤2.649 6)；区制3表示创新速度处于“快车道”(2.649 6<INS)，由此可以刻画不同区制下研发强度对上市公司价值的非线性影响。
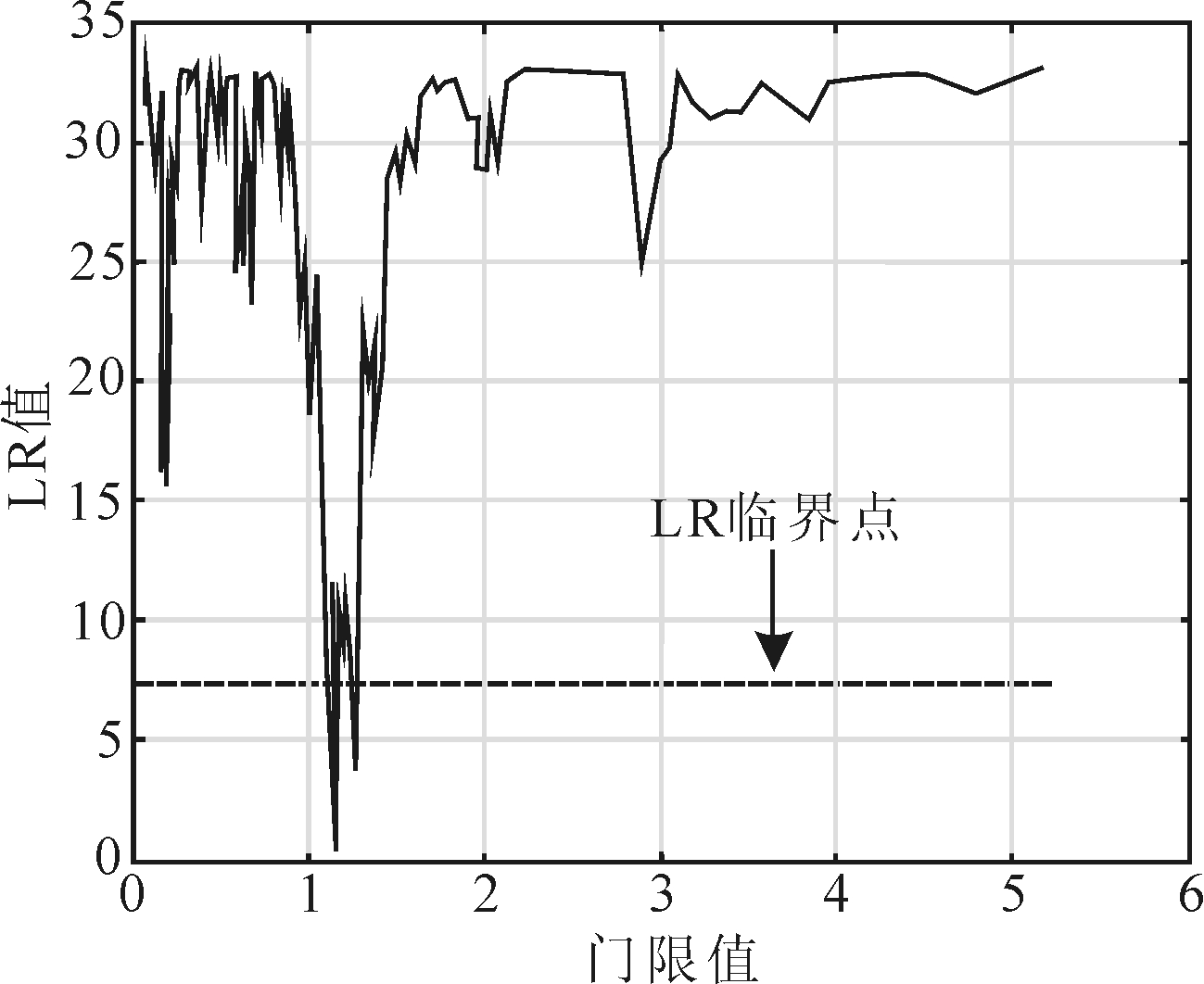
图1 双门限模型中第一门限值识别(95%置信水平)
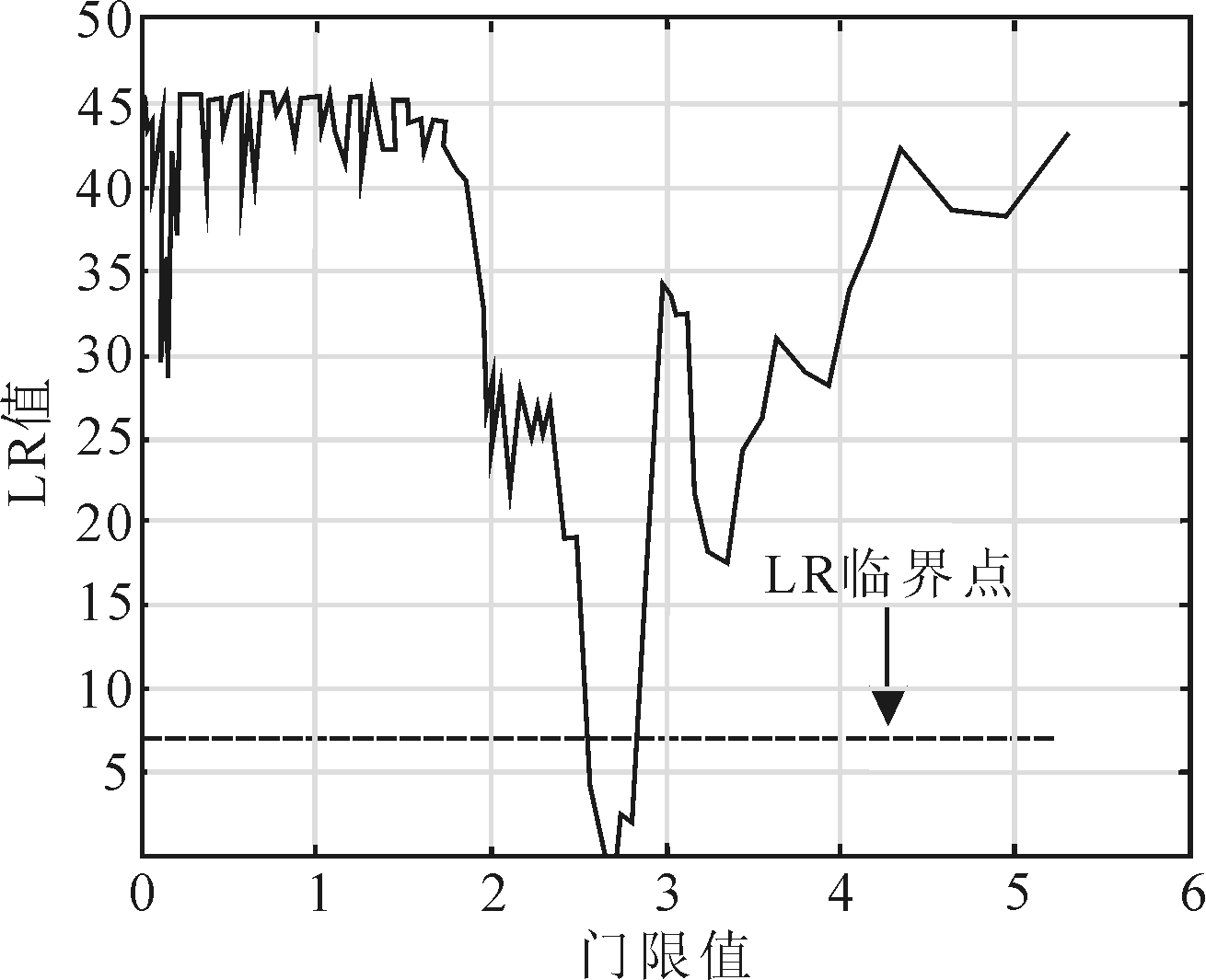
图2 双门限模型中第二门限值识别(95%置信水平)
由表5回归系数估计结果可以看出在面板线性回归模型中，研发强度的回归系数为正但不显著，表明提高研发强度对上市公司价值的提升没有显著影响。然而在面板门限回归模型中，当创新速度处于不同区制时，研发强度对上市公司价值的影响存在显著差异。具体而言，当创新速度处于“慢车道”时(INS≤1.153 3)时，研发强度与上市公司价值之间表现为负相关关系，系数为-0.183 3，且在1%水平下显著；当创新速度处于“正常行车道”(1.153 3<INS≤2.649 6)时，研发强度与上市公司价值之间仍然表现为负相关关系，但系数提高至-0.066 9，且在1%水平下显著；当创新速度处于“快车道”(2.649 6<INS)时，研发强度与上市公司价值之间转变为正相关关系，系数为0.045 9，且在1%水平下显著。这表明，当创新速度，即公司自身研发强度与同行业所有公司平均研发强度之比低于1.153 3时，公司研发强度每增强1个单位，我国上市公司价值反而下降18.33%；当创新速度介于1.153 3和2.649 6之间时，研发强度每增加1个单位，我国上市公司价值下降幅度降低为6.69%；只有当创新速度大于2.649 6时，研发强度每增加1个单位，才能带来我国上市公司价值4.59%的增长。对于中低档创新速度下增加创新投入反而不利于我国上市公司价值提升的原因,可以概括为两个方面：一方面，从产业生命周期视角，部分行业处于成熟—衰退期，创新研发空间有限；另一方面，我国股票市场发展不健全不充分，以短线投资为主，而研发强度增加的资本回报期较长，不能迅速影响上市公司价值。
表5系数估计结果
变量面板线性回归模型面板门限回归模型(双门限)RDI0.0068(0.0140)-RDI×IINS≤1.153 3()--0.183 3∗∗∗(0.028 4)RDI×I1.153 3<INS≤2.649 6()--0.066 9∗∗∗(0.018 8)RDI×I2.649 6<INS()-0.045 9∗∗∗(0.017 8)AS0.002 5(0.158 1)-0.121 2(0.179 4)SIZE-0.156 4∗∗∗(0.052 1)0.074 4(0.064 1)PB0.017 5∗∗∗(0.001 6)0.015 9∗∗∗(0.001 6)DAR-0.829 8∗∗∗(0.208 2)-0.690 4∗∗∗(0.240 3)CR-0.003 2(0.002 6)-0.002 8(0.002 8)SCR-2.649 3∗∗∗(0.448 0)-2.883 6∗∗∗(0.519 2)
注：括号中的数值表示回归系数估计值的标准差
对于本文所选取的控制变量而言，两类回归模型的参数估计结果均显示市净率与上市公司价值显著正相关；资产负债率和股权集中度与上市公司价值显著负相关，表明市净率的上升、资产负债率或股权集中度的下降会带来上市公司价值提升；资产结构和流动比率的回归系数均不显著，表明二者对上市公司价值的提升无显著作用。值得一提的是，在面板线性回归模型中，公司规模回归系数为负且在1%水平下显著，而在面板门限回归模型中，其回归系数不显著。
当公司创新速度处于中低档时，研发强度的增加并不能带来上市公司价值提升，只有公司研发强度处于同行业前列时，研发强度才会对上市公司价值产生显著正效应。为进一步剖析不同创新速度区制下的面板数据特征，本文基于所选819家上市公司共计573 3个样本数据，以创新速度不同区制为主要划分依据，计算样本上市公司不同年份划入不同区制的百分比。具体而言，对于特定年份t，上市公司划入不同区制的百分比计算公式为：
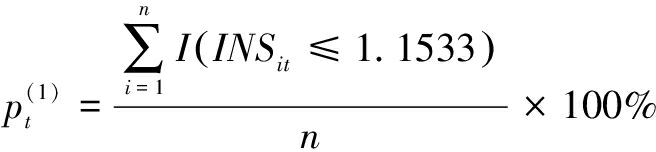
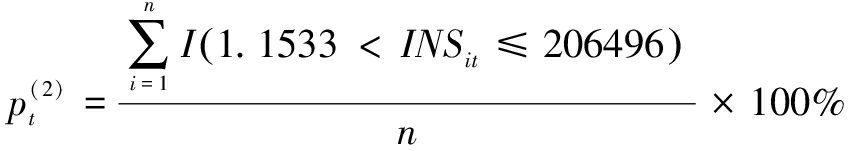
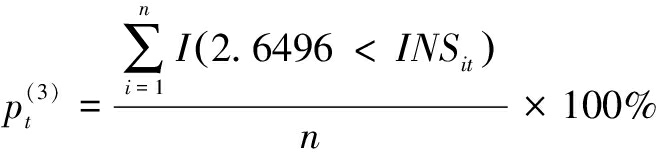
(19)
其中，
和
分别表示上市公司在年份t划入区制1、区制2、区制3的百分比；INSit表示公司i在年份t的创新速度；n表示上市公司总数。
表6显示，从区制角度看，我国A股上市公司有近六成创新速度处于“慢车道”，创新动力不足，研发投入量不容乐观；约三成公司的创新速度处于“正常行车道”；而创新速度驶入“快车道”，研发强度位于行业前列的公司仅在10%以下。从时间角度来看，我国A股上市公司在不同年份划入不同区制的百分比基本稳定，但总体来说随着时间推移，创新速度驶入“慢车道”的公司占比有上升趋势，而创新速度驶入“快车道”的公司占比出现下降现象。可见，我国股票市场发展近30年来，虽然体量巨大，发展速度超前，但上市公司创新能力、研发强度并不乐观。
图3呈现了2010-2016年不同行业上市公司在不同区制下的分布状况，限于篇幅，此处仅展示加权排序后各区制下占比前三的行业。
表62010-2016年上市公司在各区制百分比(%)
区制2010201120122013201420152016INS≤1.153 3606066646864671.153 3<INS≤2.649 6303128322729282.649 6<INS101064565
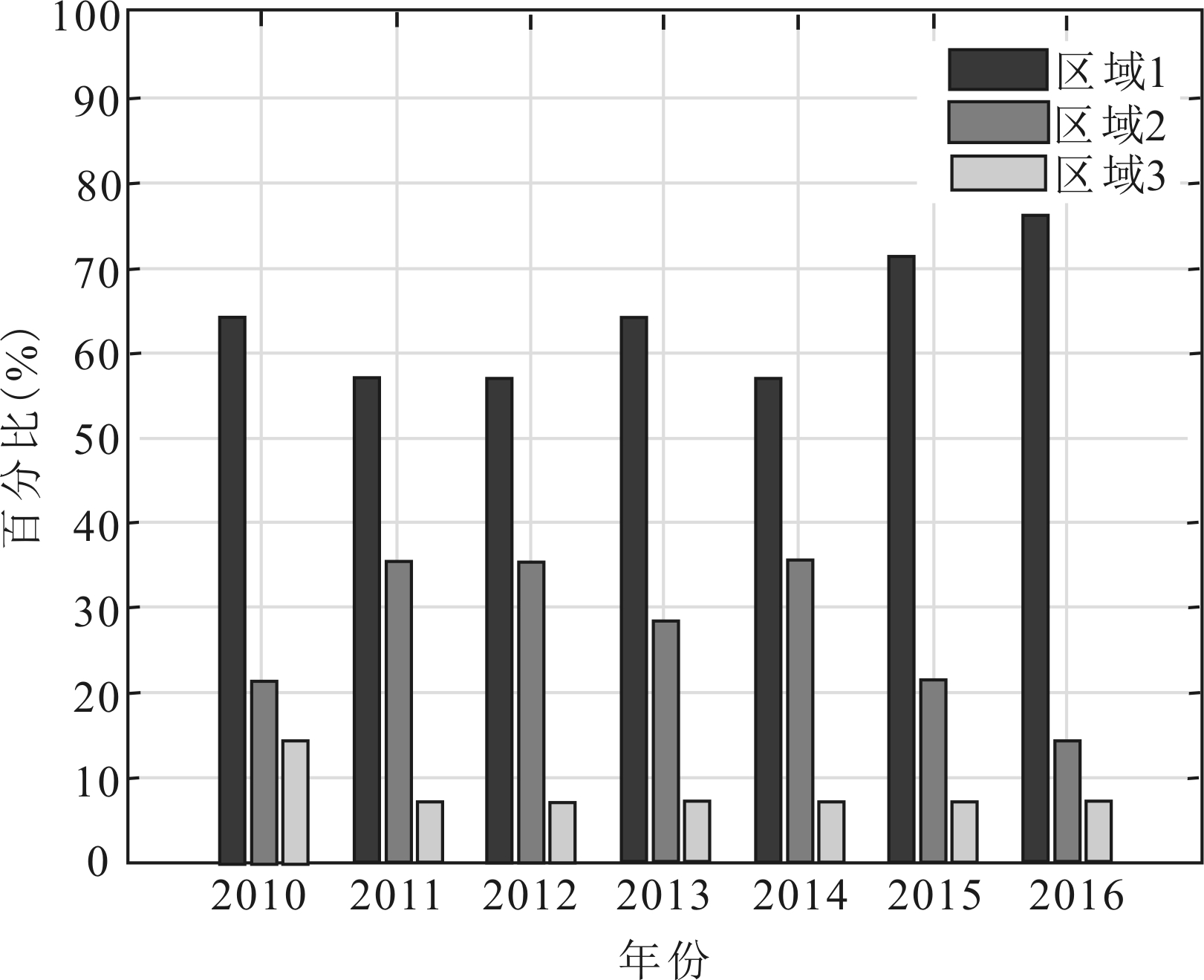
(a)农、林、牧、渔业
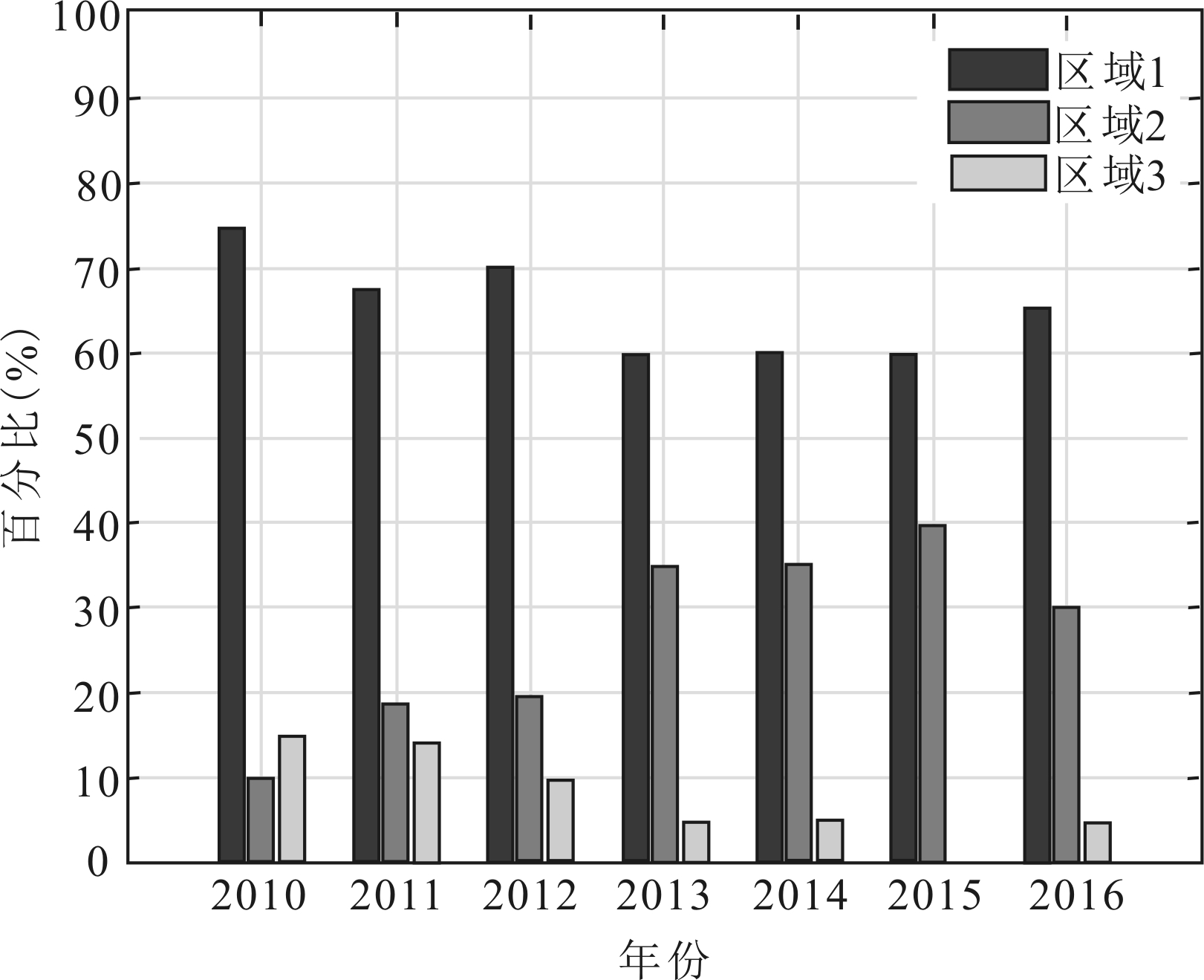
(b)采矿业
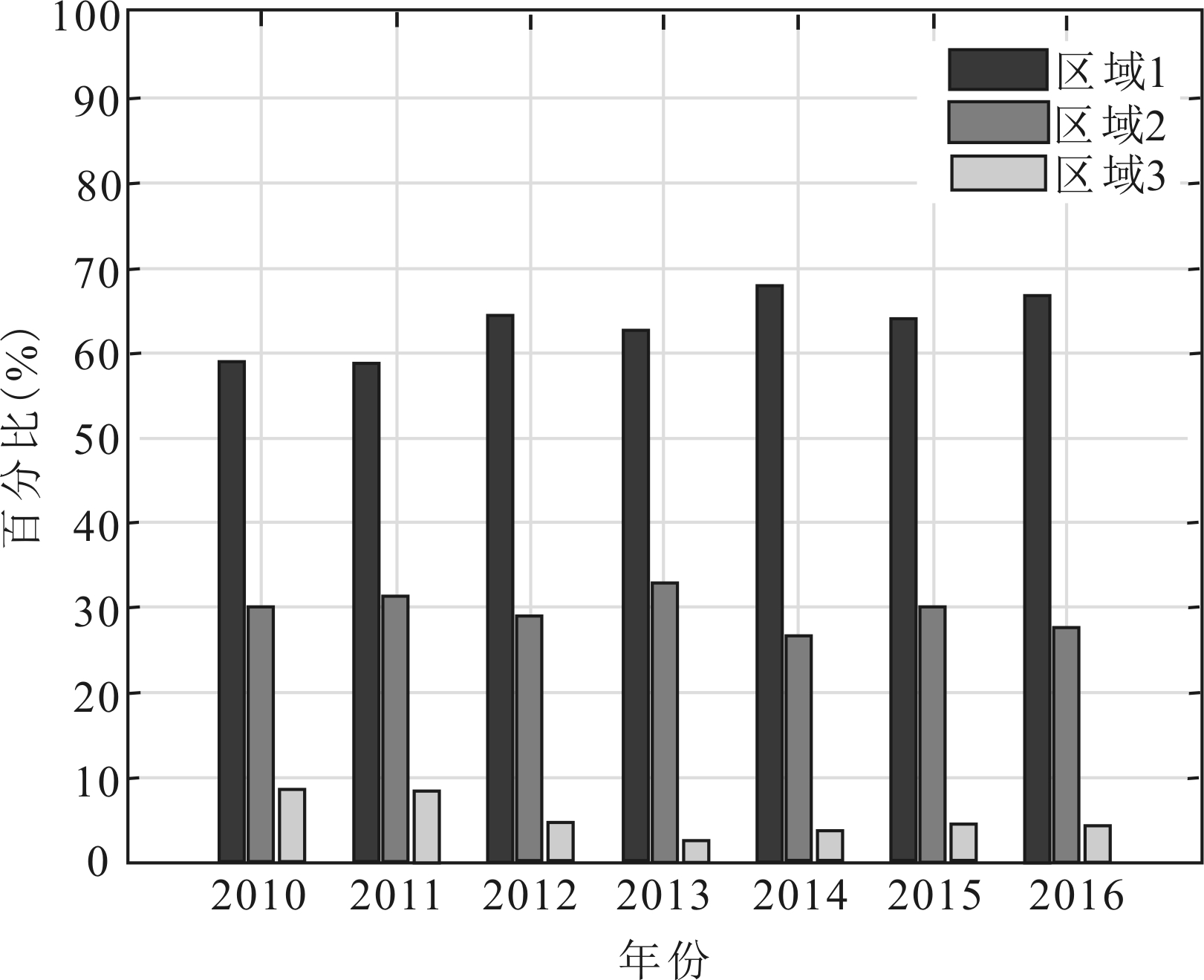
(c)制造业
图3不同行业上市公司在不同年份与不同区制下的百分比
从行业角度来看，农林牧渔业和采矿业的公司大多处于创新速度的“慢车道”，缺乏创新活力。按照企业生命周期理论，这两类产业大多处于成熟—衰退期，研发创新空间有限，基于公司价值考量，研发投入的战略决策也相对保守。相比之下，批发零售业、电力、热力、燃气及水生产和供应业的公司创新速度处于“快车道”的明显较多。一方面，随着互联网发展，传统批发零售业在运营模式上不断更迭，对研发投入的需求量大幅增加；另一方面，能源供应类企业大多拥有国有资产成分，其能源输送供应设备科技含量较高，研发强度也相对较高。特别地，由图3可知，所选样本中，超五成制造业公司创新速度处于“慢车道”，处于“快车道”的公司数量甚至与同条件下农林牧渔业公司水平不相上下。这说明我国制造业转型升级压力依然较大，制造业技术水平不高，创新乏力。此外，信息传输、软件和信息技术服务业公司创新速度差距显著，呈现出强者恒强的局势。产品科技含量是信息产业的命脉，缺乏足够的研发投入，创新驱动力不足会严重抑制企业发展壮大。
从时间角度来看，采矿业、制造业、批发和零售业变化幅度相对较小。农林渔牧业中创新速度处于“慢车道”的公司占比整体呈上升趋势，创新能力触顶。电力、热力、燃气及水生产和供应业公司的创新速度差距不断缩小，尤其是2016年，处于“正常行车道”的公司首次超过了处于“慢车道”的公司，这类公司在研发投入增加的同时也承担着公司价值降低的风险。信息传输、软件和信息技术服务业不同公司之间的创新速度差距依然存在，但逐渐变小。
本文基于2010—2016年我国A股上市公司面板数据，借助Hansen[10]提出的面板门限回归模型，对我国研发强度、创新速度与上市公司价值之间的关系进行了定量研究。本文在充分考虑研发创新活动特性与趋势的基础上，使用公司自身研发强度与同行业所有公司平均研发强度的相对数，即创新速度，作为门限变量，利用翔实的样本数据对研发强度与上市公司价值之间的非线性关系进行了实证研究。根据实证分析结果，本文研究分析结论归纳如下：
(1)研发强度对上市公司价值存在双重门限效应。当上市公司研发强度与行业研发强度之比低于1.153 3时，即上市公司创新速度处于“慢车道”，研发强度与上市公司价值存在显著负相关关系；当上市公司研发强度与行业研发强度的比重介于1.153 3～2.649 6时，即上市公司创新速度处在“正常行车道”，研发强度对上市公司价值的负向影响力度降低；当上市公司研发强度与行业研发强度的比重达到2.649 6以上时，即上市公司创新速度驶入“快车道”，研发强度提高将带来上市公司价值提升。
(2)市净率对市场价值具有显著正效应，资产负债率的降低会引发市场价值的提升，公司股权集中度与市场价值显著负相关。合理控制资本结构，优化股权结构，依靠优良业绩增加公司利润，有助于我国上市公司不断壮大。
(3)我国A股市场的研发强度、创新速度不容乐观。从不同创新速度区制来看，近六成企业处于创新“慢车道”，仅约一成的企业成功跻身创新“快车道”，真正依靠研发投入为企业创造市场价值。此外，我国A股上市公司在不同年份落入不同区制的百分比在行业间存在明显差异。
当创新速度处于不同区制时，研发强度对上市公司价值的影响存在显著差异，这表明无论是公司内部，还是政府部门、行业监管部门应当齐心协力。公司股东应当充分认识创新速度对公司发展的重要意义，不能因为研发投入资金需求量大就固步自封。尤其应当改变高层管理者的绩效评定方式，将创新速度、研发强度、研发成果纳入考核指标，同时对员工创新给予激励。改善经营权与管理权分离带来的公司高管追求营业收入，不重视长远发展的代理问题。政府应当出台相应的税收优惠政策，研究制定科学合理的抵扣、减免税法，同时完善企业研发成果评价体系，对于真正将股东资本用于研发的企业进行大力扶持，对于弄虚作假套取税收优惠的企业予以惩处。同时，要进一步鼓励高校科研人员参与公司产品研发、营销创新和管理优化，为企业创新速度由“慢车道”换挡提速到“快车道”提供驱动力和润滑剂。证券监管部门应进一步要求公司披露相关研发创新活动，增强对中小股民的引导，鼓励中小股民开展长线投资，注重企业创新能力。完善兼并收购、借壳上市以及退市制度，为真正创新的企业减少融资障碍，让创新乏力业绩不佳的企业退出市场。
为保证数据真实、准确，本文剔除了部分数据残缺的公司样本，样本中缺少金融业、卫生与社会工作行业公司，这可能是本文研究欠缺之处。此外，上市公司价值影响因素众多，创新能力指标仅是其中一个方面，现有研究中对资本结构与公司价值的研究日益增多，创新能力、资本结构能否共同影响公司价值是笔者今后重点研究的方向之一。
[1] 项云帆.研发强度对上市公司市场价值的门槛效应[J]. 科技进步与对策, 2015, 32(11): 83-86.
[2] 项云帆.公司创新投入、创新速度及激励选择[J]. 财会月刊, 2016(30): 11-17.
[3] STALK G. Time the next source of competitive advantage[J]. Harvard Business Review, 1988, 66(4): 41-51.
[4] MANSFIELD E. Industrial R&D in Japan and the United States: a comparative study[J]. The American Economic Review, 1988, 78(2): 223-228.
[5] MURMANN P A. Expected development time reductions in the German mechanical engineering industry[J]. Journal of Product Innovation Management, 1994, 11(3): 236-252.
[6] 王新春, 戚桂杰, 梁乙凯, 等. 开放式创新社区组织知识创造能力提升研究[J]. 情报杂志, 2016, 35(3): 203-207+202.
[7] GARNER J L, NAM J, OTTOO R E. Determinants of corporate growth opportunities of emerging firms[J]. Journal of Economics and Business, 2002, 54(1): 73-93.
[8] TONG H. On a threshold model in pattern recognition and signal processing[M]. Amsterdam: Sijthoff and Noordhoff, 1978.
[9] TONG H, LIM K. Threshold autoregression, limit cycles and cyclical data[M]. Exploration of a Nonlinear World: An Appreciation of Howell Tong's Contributions to Statistics,1980.
[10] HANSEN B. Threshold effects in non-dynamic panels: estimation, testing, and inference[J]. Journal of Econometrics, 1999, 93(2): 345-368.
[11] CHAN K S. Consistency and limiting distribution of the least squares estimator of a threshold autoregressive model[J]. Annals of Statistics, 1993, 21(1): 520-533.
[12] HANSEN B. Inference when a nuisance parameter is not identified under the null hypothesis[J]. Econometrica, 1996, 64(2): 413-430.
[13] BAI J. Estimating multiple breaks one at a time[J]. Econometric Theory, 1997, 13(3): 315-352.
[14] LIN B, LEE Y, HUNG S. R&D intensity and commercialization orientation effects on financial performance[J]. Journal of Business Research, 2006, 59(6): 679-685.
[15] LEVIN A, LIN C F, CHU C. Unit root tests in panel data: asymptotic and finite-sample Lewis, properties[J]. Journal of Econometrics, 2002(108):1-24.
[16] IM K S, PESARAN M H, SHIN Y. Testing for unit roots in heterogeneous panels[J]. Journal of Econometrics, 2003(115):53-74.