0 引言
专利是现代技术创新成果的重要载体,专利公开制度成为技术扩散的驱动力,极大地推进了全社会技术进步。专利引用为跟踪、评估甚至预测技术扩散提供了最有效的显性线索[1],沿着专利引用路径可以发现知识来源与去向,揭示技术之间的传承、关联,有助于认知技术扩散背后隐藏的技术创新机理。
技术扩散现象早已被学界关注。首先,以mansfield[2]、Jaffe[3]为代表的早期学者在技术-经济框架下探讨了技术扩散,尤其揭示了知识溢出效应,肯定了技术扩散对创新型经济的积极作用。其次,技术扩散动力机制受到重视,以Bass、Logistic、Gompertz等为代表的技术扩散模型得到了广泛探讨。值得注意的是,网络科学、复杂系统理论为技术扩散建模提供了启发,例如企业组织网络技术扩散[4]、技术扩散与网络结构演化[5]、高校与上市公司技术扩散网络模型[6]、合作网络技术扩散[7]。最后,也有学者侧重于数据驱动的实证研究,通过科学计量指标、数据挖掘方法,从专利大数据中发现创新动态。
梳理相关文献,发现技术扩散研究存在以下不足:①基于数学模型的仿真研究较多,但实证研究不多;②已有实证研究多偏重于相关性分析,对于专利技术扩散影响因素的系统性定量研究不足;③从网络视角研究专利技术扩散的文献多,但很少考虑专利技术扩散路径间相关性,尤其缺乏结构嵌入导致的网络内生性影响研究。
鉴于上述问题,整合已有研究成果,从网络系统视角构建包含内生因素、外生因素两个层面的分析框架,将专利技术扩散影响因素归纳为专利价值、专利保护、多维同配、结构嵌入4个方面,并以石墨烯为实证领域,采用随机指数图模型进行实证分析,旨在揭示技术扩散多元机制。
1 分析框架与研究假设
1.1 分析框架
专利引用反映了从被引专利到施引专利的技术扩散,扩散路径相互连接,形成网络结构。技术扩散的主体、行为、影响都依赖于网络嵌入环境,某种程度上,透过网络可以认知技术扩散内在本质[8]。从网络系统角度,可以将专利技术扩散因素抽象为两类:一是内生性因素,即结构嵌入;二是外生性因素,即节点属性和边属性。结构嵌入是指网络边形成的某种特定模式,是社会网络分析中常见的研究对象。值得注意的是,形成特定网络结构背后的动力机制可能对认识技术扩散网络具有重要理论意义。结构嵌入本质上反映了网络边的自相关性,即每条边不是孤立存在的,而是受到其它边的影响。例如,拥有共同节点P的两条边(O、P)、(P、Q),考虑到P的中介效应,两条边的存在与否必然相互影响与依赖。由此,结构嵌入对网络产生内生性影响。网络节点属性、网络边属性对网络具有外生性影响。
将专利技术扩散影响因素纳入上述分析框架,旨在从网络内生与外生两个层面考察专利技术扩散形成机制。整合有关理论及研究成果,将专利技术扩散机制归纳为4个方面:专利价值、专利保护、多维同配、网络嵌入,如图1所示:①以创新理论为指导,认为专利价值和专利保护直接影响了专利成为技术扩散源的难易程度。同时,选择专利被引、保护强度为相应代理变量,在度量模型中,它们被视为扩散网络节点属性,属于外生变量;②以知识溢出理论为指导,认为多维同配有利于技术扩散。本文从技术、地理、组织3个层面表征专利同配性,多维同配变量本质上为二元关系,在度量模型中被视为节点二元属性,属于外生变量;③以社会网络理论为指导,技术扩散路径倾向于嵌入某种网络结构中。这里重点考察三角结构,相应变量在度量模型中被视为网络构型,属于内生变量。
1.2 研究假设
(1)专利价值。专利价值来源于两个层面:一是反映技术进步、产品工艺改进;二是反映专利在市场、经济层面的价值,包括排他性的经济收益权、市场竞争工具。在知识产权制度完善国家,专利价值已经超出技术范畴,具有提升竞争力的战略性功能[9],例如防御或进攻型阻挡、谈判筹码、企业声誉、吸引资本、市场开拓、内部激励等。专利价值直接影响发生技术扩散的可能性,即专利价值越高,对其他创新主体的吸引力越大,就越容易被竞争对手学习、模仿甚至侵权(叶芬斌,2002)。高价值专利通常表现出高被引现象,意味着更容易成为技术扩散源头。基于以上分析,本文提出以下研究假设:
H1:专利价值促进了技术扩散,即专利价值越高,就越可能成为技术扩散源。
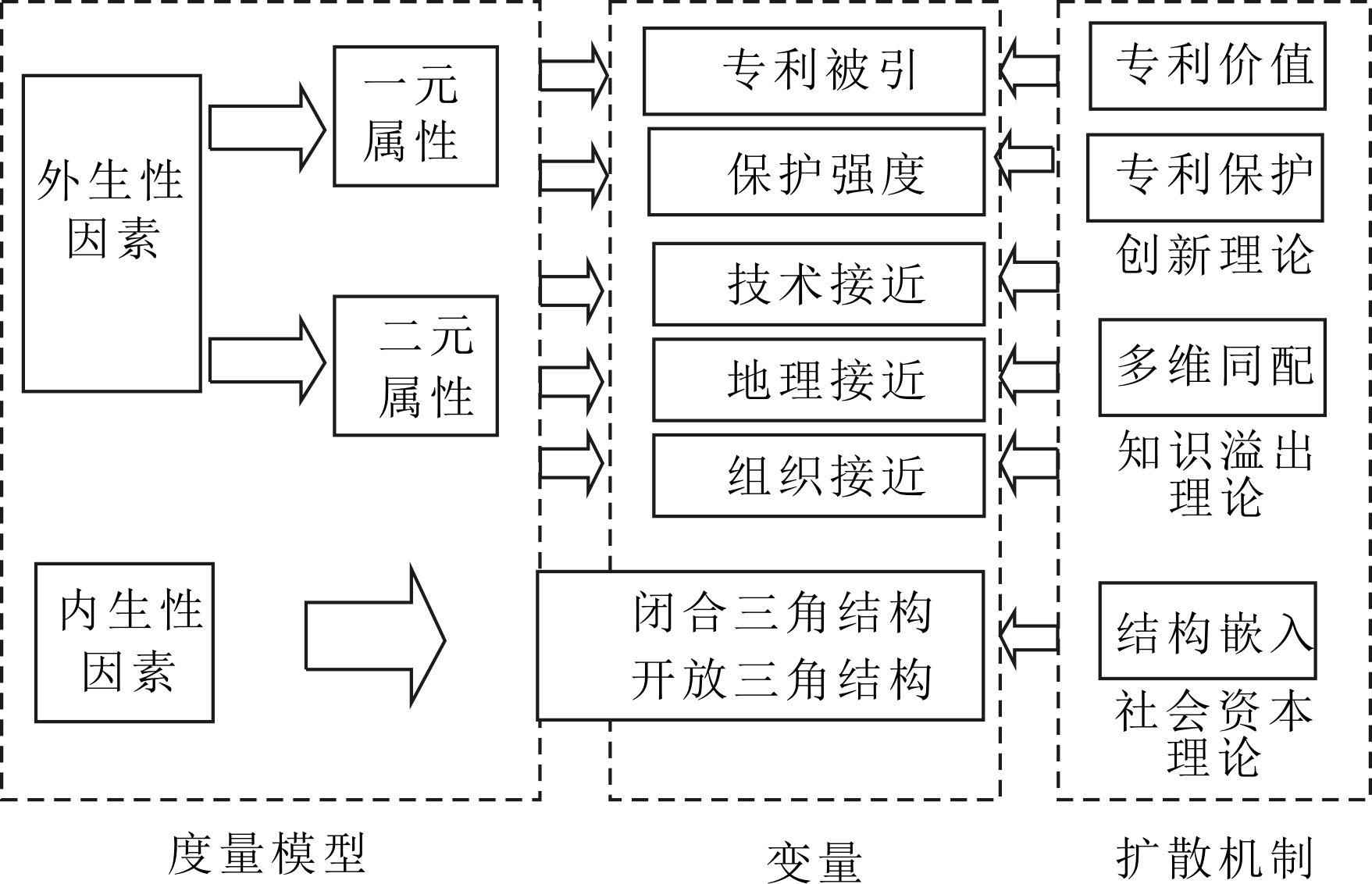
图1 理论分析框架
(2)专利保护。专利保护是指专利权人对专利技术经济收益的独占程度。按照新古典经济学理论,专利保护制度的理论基础来源于知识产品特性引致的市场失灵问题[10]。例如,Arrow[11]指出,由于知识的正外部性和溢出效应,市场价格难以反映新知识的真实价值,社会收益远远超出了私人收益,导致创新投入不足。因此,为了弥补创新成本、激励研发投入,有必要通过行政手段赋予创新主体一定时期的垄断权,以解决市场失灵问题。
但是专利保护具有双面性。从全社会角度出发,专利保护影响和限制了技术知识扩散,甚至可能损害公共福利。例如,Mansfield等[2]针对化学、制药、电子、机械工业领域的实证发现,专利制度使技术模仿成本提高了约11%。实践中,企业可以通过多种专利战略达到不同程度的技术扩散抑制效果,常见方式包括:主张全面的专利权利要求,例如在权利要求中对技术保护细节的详细描述;要求宽泛的专利技术领域代码;在核心专利周边申请更多其它专利,形成专利“围墙”或“丛林”;提高专利转让门槛,要求高额的专利许可费用[12]。不论是理论还是实践层面,说明在加强专利权人收益保护的同时,不能忽视技术排他性、经济垄断性导致的社会福利损失,尤其是对技术扩散的抑制效应。基于以上分析,本文提出以下研究假设:
H2:专利保护抑制了技术扩散,即保护强度越大,技术扩散机会就越小。
(3)多维同配机制。技术扩散可能跨技术领域[13]、跨地理空间[14]、跨组织边界[15],这些因素制约专利技术扩散。有文献指出,技术、地理、社会层面的接近有利于专利技术扩散。
技术同配。技术同配是指专利技术的领域分布,相同领域专利在技术功能、知识要素、基本原理方面存在相似或接近性。技术同配代表技术接近性,同质性知识更有利于创新主体对外部知识的获取与吸收,降低了技术扩散门槛。因此,技术同配促进了专利技术扩散。
地理同配。地理同配是指专利所有权人位于相同的地理空间。地理空间接近意味着创新资源的集聚,以Jaffe[16]为代表的学者证实了创新主体在地理空间集聚有利于知识扩散。空间距离缩短有利于研发人员面对面交流,更有利于隐性知识溢出和吸收。源于相同城市的专利权人更容易建立联系,形成并维持关系的成本低,因而更有利于专利技术扩散。
组织同配。组织同配指专利所有权人属于相同创新组织。作为创新活动的组织形式,高校及科研机构内部创新人员之间存在着密集的社会网络,形成的内部强关系为技术扩散提供了高效的知识流渠道,不但易于显性知识传播,更重要的是低成本、便利化的非正式交流所引致的隐性知识溢出效应(孙德忠等,2014)。源于相同组织的专利技术具有更高的内部曝光度、信任度,在技术上拥有更强耦合性,更容易产生专利技术扩散。综上所述,本文提出如下假设:
H3:技术、地理、组织层面的同配性有利于专利技术扩散。
(4)结构嵌入机制。结构嵌入是指专利技术扩散倾向于嵌入某种网络结构。近年来,结构嵌入已经成为创新研究领域的重要议题。学界普遍认识到创新活动往往根植于本地的制度、文化、关系环境之中,网络嵌入对于创新行为具有独特影响,对于个体可能是难以简单模仿和移植的竞争优势[17]。按照开放式创新理论,网络结构嵌入反映了创新的社会建构性,创新并不完全是封闭性的个体革新行为,而是具有社会性,某种程度上是社会要素交互的结果[18]。因此,网络结构是技术扩散多元复杂要素交织的宏观涌现,反映了技术创新的内在根本动力。对于技术扩散网络,虽然已有丰富的研究成果,但大多只是停留在拓扑结构的简单统计层面,难以深刻揭示背后的因果机制。
按照社会网络理论,专利技术扩散不是孤立事件,扩散路径之间存在相互影响和依赖,这种相关性会导致扩散路径构成某种特定结构。在有向网络中,传递三角结构是一种基本模式,即如果节点i连接节点j,节点j连接节点k,则节点i很有可能也会连接节点k。在专利技术扩散网络中,两个专利间可能同时存在冗余扩散路径,包括直接路径与间接路径,间接路径表现为通过第三方专利的中介功能建立长度为2的间接连接[19]。嵌入三角结构意味着:如果两个专利间存在间接技术扩散路径,则它们之间很可能会建立直接技术扩散路径,形成传递三角结构。基于以上分析,本文提出如下假设:
H4:专利技术扩散倾向于嵌入传递三角结构。
2 研究方法
2.1 指数随机图模型
指数随机图模型(ERGM)是针对网络建模形成的定量分析方法,关注于各种网络变量对网络边生成的影响效应。一般地,模型刻画了从随机网络集合Y中观察到一个实际网络y的概率,这个概率的大小依赖于各种所谓的网络构型(Configuration),构型可以是网络中可能会出现的某种结构模式,如边、三角结构、星型结构。模型中设定观察到网络y的概率为因变量,各种网络构型作为自变量,一般化模型形式如式(1)所示[20]。
![]()
(1)
其中,Y是网络中二元关系(有边或无边)的随机集合,y是关系的特定实现。X是边或节点相关的协变量向量。θ是对应于各种网络构型的系数向量,其大小反映了网络构型对于网络形成的作用效应。g(y, X)是由被纳入模型的网络构型统计量构成的向量,如果某构型在网络y中被观察到k次,则g(y)=k。κ(θ,y)是归一化因子,用以确保所有可能网络样本出现的概率和为1,即∑z∈Yexp{θTg(z,X)}=1。
(2)
其中,函数logit代表对数几率,定义为![]() 代表除了网络边Yij之外的网络Y的其余部分。式(2)左边代表网络其余部分
代表除了网络边Yij之外的网络Y的其余部分。式(2)左边代表网络其余部分![]() 不变的情形下,节点i和j建立连接的对数几率。固定网络其余部分不变,当yij由0变为1时,网络统计量g(yij)每增加1个单位,则i和j建立连接概率与不建立连接概率的比值为exp(θ),或者说对数几率为θ。参数θ大小反映相应网络构型对边的边际效应。
不变的情形下,节点i和j建立连接的对数几率。固定网络其余部分不变,当yij由0变为1时,网络统计量g(yij)每增加1个单位,则i和j建立连接概率与不建立连接概率的比值为exp(θ),或者说对数几率为θ。参数θ大小反映相应网络构型对边的边际效应。
指数随机图模型适用于本文研究问题:①模型适用性强,将专利视为节点,专利引用视为网络边,则可以将专利技术扩散影响因素问题转化为网络建模问题;②能够分析网络系统中因果关系,满足网络影响因素定量化分析要求;③能够捕捉结构对网络的影响效应,克服网络边自相关带来的拟合困难。
2.2 模型变量
表1列出了实证模型中用到的有关变量,包括类型、图例、含义。具体地,网络嵌入通过构型变量表达,优先连接通过节点一元变量表达,多维同配通过节点二元变量表达。
2.2.1 专利价值变量
有多种判断专利价值大小的方法,例如诉讼、专利簇、专利维持、科学关联,被引数量是其中应用最为广泛和有效的指标。申请者及审查者为了说明技术间区别与关联而引用其它专利,通常认为技术新颖或商业前景巨大的专利会受到更多的曝光和重视。因此,专利被引数tc是专利价值的合适代理变量。如果模型中Nodeicov(tc)系数显著为正,则说明专利价值很高,发生技术扩散的可能性就更大。
表1 有关ERGM模型变量类型
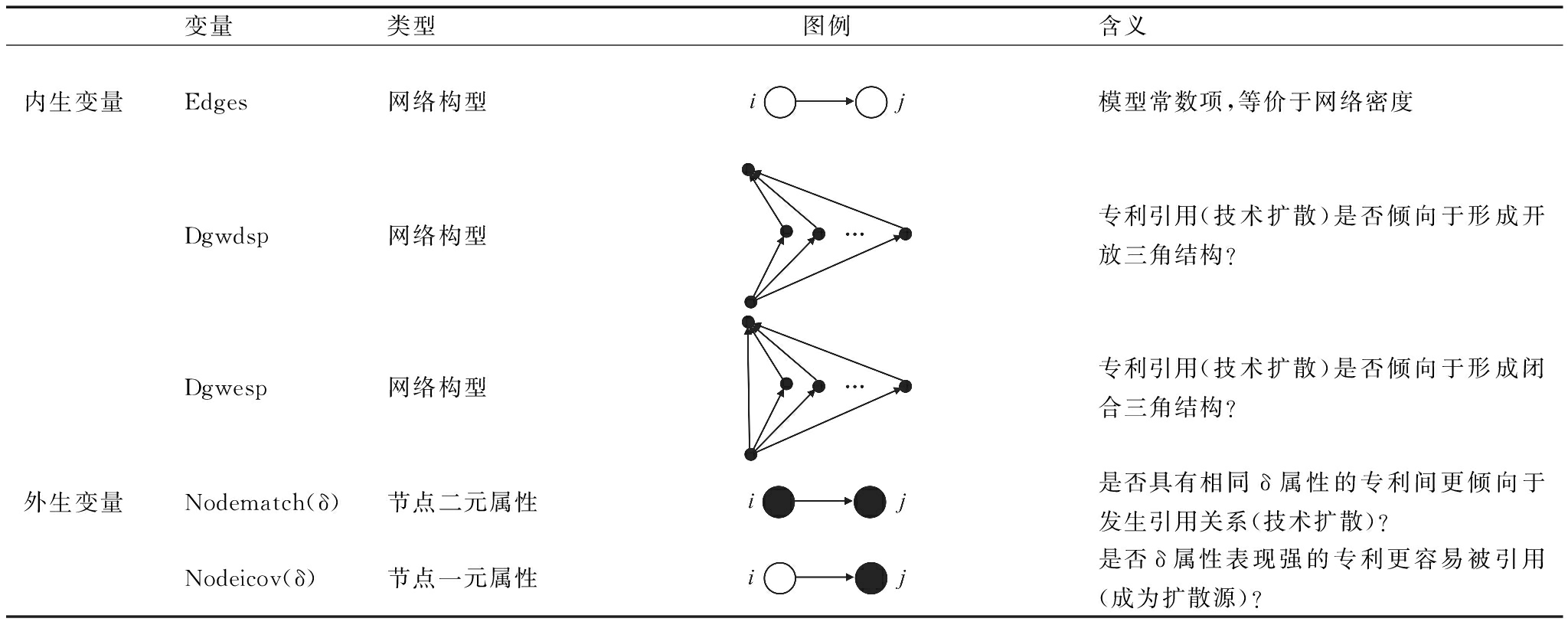
变量类型图例含义内生变量Edges网络构型模型常数项,等价于网络密度Dgwdsp网络构型专利引用(技术扩散)是否倾向于形成开放三角结构?Dgwesp网络构型专利引用(技术扩散)是否倾向于形成闭合三角结构?外生变量Nodematch(δ)节点二元属性是否具有相同δ属性的专利间更倾向于发生引用关系(技术扩散)?Nodeicov(δ)节点一元属性是否δ属性表现强的专利更容易被引用(成为扩散源)?
2.2.2 专利保护变量
专利宽度是表征专利保护强度的常见指标。专利本质上是一种通过技术声明保护而获得的经济收益权利,专利声明保护范围体现了技术保护强度,每个专利都被划分到多个IPC分类领域,被审查认定的领域越多,说明专利技术的潜在应用和保护范围越广。IPC分类是一种分层结构技术体系,按照技术主题设立类目,在编码上由部、大类、小类、大组、小组构成。本文将专利宽度width定义为专利的IPC小类数量。如果模型中Nodeicov(width)系数显著为负,则说明专利保护强度抑制了技术扩散。
2.2.3 多维同配变量
(1)地理同配。本文采用一种简单、直接的方法表征地理接近性,即专利的国家匹配关系。专利文献中明确标明了专利申请者的来源国家,如果专利所有权人来自相同国家,就认为具有高度地理接近性,否则相反。模型中用变量Homo(cy)表征地理同配,如果其系数显著为正,则说明源于相同地理国家的专利技术更容易发生技术扩散。
(2)组织同配。专利发明者通常通过两种形式实现创新活动,一是利用组织公共资源开展的职务发明,专利权利人为所属机构;二是个人私下的发明成果,专利权利人为个人。因此,可以通过专利权利人(Assignee)判断专利技术的来源组织。如果两个专利具有相同的专利权人(机构或个人),则认为存在组织同配关系,否则相反。模型中用变量Homo(ass)表征组织同配,如果其系数显著为正,则说明源于相同组织的专利技术更容易发生技术扩散。
(3)技术同配。专利文献标明了多个可能技术领域,如通用的国际技术分类表IPC,其中最重要领域为主IPC分类。具体地,如果专利主IPC分类号的前四位相同(IPC小类相同),则认为具有技术同配关系,否则相反。模型中用变量Homo(ipc)表征技术同配,如果其系数显著为正,则说明源于相同技术领域的专利技术更容易发生技术扩散。
2.2.4 网络嵌入变量
两个反映网络结构的变量被用于刻画三角嵌入倾向,即几何加权二元关系共享伙伴Dgwdsp(geometrically weighted dyad-wise shared partners)和几何加权边共享伙伴Dgwesp(geometrically weighted edge-wise shared partners),如表1所示。上述两个变量既能够刻画网络嵌入倾向,又可以防止模型退化问题[21]。
变量Gwdsp用于刻画一种网络连接倾向,即节点不直接连接而至少存在1条长度为2的间接连接。在专利引用网路中,该变量捕捉了开放三角结构模式,即专利i引用专利j,专利j引用专利k,而专利i和专利k之间不存在引用关系。变量Dgwesp表征了网络中边组成的三角结构数量,且这些三角结构共享相同的节点对。这个变量捕捉了经典的传递三角结构,即专利i引用专利j,专利j引用专利k,而专利i亦引用专利k。如果变量Dgwesp系数为正、Gwdsp系数为负,则说明专利技术扩散更可能形成闭合传递三角结构,而不是开放三角结构。网络内生性变量Dgwesp、Dgwdsp本质上捕捉了扩散路径之间的依赖性,反映了技术扩散结构嵌入倾向。
3 实证分析
3.1 数据来源与描述分析
本文选取石墨烯为研究领域,以美国授权专利数据库(PatFT)为检索工具获取数据。检索专利标题或摘要中包含有关键字“graphene”的记录,检索式为“ttl/graphene or abst/graphene”,检索时间为2017年7月,最终得到数据1 800条。利用专利抓取程序从网站系统抽取相关专利内容及属性,用于变量计算。抽取每个专利文本的元信息,主要包括引用、专利权人、来源国家、IPC号,上述信息用于计算形成专利扩散网络及模型的变量。
专利引用是本文跟踪技术扩散的关键手段,通过引用关系构建技术扩散网络。具体地,抽取专利文本的引用(Reference)项,存在数据集内部引用关系的专利652件,构建652×652的邻接关系矩阵,形成模型因变量。从网络拓扑结构看,低密度(0.002)、低全局聚类系数(0.013)特征说明网络较为稀疏,反映出石墨烯领域处于技术扩散初期。
表2给出了指数随机图模型中有关变量特征:①专利价值变量。专利价值均值较低(1.138),主要原因在于石墨烯领域存在大量新授权专利,引用时滞效应一定程度上导致专利价值被低估;②专利保护变量。该领域专利保护强度较高,平均每个专利约覆盖4个IPC小类;③多维同配变量。施引专利与被引文献之间呈现高度的多维同配倾向,国家同配率达到66%,技术领域同配率为48%,专利权人同配率为23%。深入分析发现,技术扩散同配现象主要集中在少数创新主体范围内,如国家同配主要集中于美国、韩国,研发机构同配主要以IBM、SAMSUNG、NANOTEK为代表,技术同配主要集中在H01L、C01B为代表的IPC小类;④结构嵌入变量。三角结构是研究扩散网络嵌入的主要模式。样本网络有闭合三角结构23个,开放三角结构83个,反映出技术扩散路径之间的依赖模式。
表2 模型变量描述

变量特征数量边数742专利价值均值1.138专利宽度均值3.949相同所属国家491(66%)相同专利权人170(23%)相同技术领域359(48%)闭合三角结构23开放三角结构83
3.2 结果分析
采用R环境中的STATNET程序包进行模型参数估计,估计方法采用马尔可夫链蒙特卡罗最大似然估计法(MCMC MLE)。另外,通过AIC和BIC指标可以判断模型拟合程度,数值越小说明模型越佳;通过t统计量可以判断单个变量的显著性。
表3给出了模型拟合结果,模型1、模型2、模型3分别单独检验了H1和H2、H3和H4,H4则加入了所有变量,检验了所有因素的技术扩散效应。总体上,各个模型变量都通过了显著性检验,加入全部变量的模型4在AIC和BIC指标上表现更卓越,与前3个模型参数拟合结果基本一致,初步说明模型变量选择恰当、拟合效果好。接下来,具体给出4个模型的拟合结果。
模型1旨在检验是否是高专利价值、弱保护强度的专利更容易成为技术扩散源头。变量Nodeicov(tc)系数显著为正,意味着专利价值每增加1个单位,被引用几率增加到1.12(=e0.11)倍,反映出专利价值对技术扩散的正向影响。变量Nodeicov(width)系数显著为负,意味着专利宽度每增加1个IPC小类领域,被引几率增加到0.81(=e-0.215)倍,小于1的几率值说明保护强度对技术扩散具有反向影响。模型1结果说明,专利价值越高、保护强度越低,专利越容易被引用,越容易成为技术扩散源。总之,实证结果支持H1、H2。
模型2旨在检验多维同配能否促进技术扩散。变量Homo(ipc)、Homo(cy)、Homo(ass)系数均显著为正,说明技术、地理、组织层面同配性促进了专利技术扩散。如果单独考虑某种同配因素,技术扩散发生于国家内部的概率是跨国的1.76(=e0.563)倍;技术扩散发生于组织内部的可能性是跨组织的3.04(=e1.113)倍;技术扩散发生于技术领域(IPC小类)内部的概率是跨技术领域的2.7(=e0.994)倍。如果同时考虑3种同配因素,技术扩散同时呈现技术、地理、组织同配的概率是异配的14.44(=e0.563+1.113+0.994)倍。总之,实证结果说明,多维同配机制促进了专利技术扩散。其中,组织同配效应最强,技术同配次之,地理同配最弱,支持H3。
模型3旨在检验技术扩散路径是否倾向于嵌入三角结构。变量Dgwesp系数显著为正,意味着保持扩散网络其它部分不变,嵌入闭合三角结构的概率是嵌入其它结构的63.12(=e4.145)倍,说明技术扩散有强烈的倾向嵌入闭合三角结构。变量Dgwdsp系数显著为负,说明技术扩散并不倾向于形成开放三角结构。模型3结果说明专利技术扩散路径倾向于嵌入闭合三角结构,支持H4。
模型4旨在考察实证结果的稳健性。通过比较可以发现,模型4的结果与上述3个模型的结果保持一致,说明模型设定合理。值得注意的是,变量Dgwesp的边际效应非常强,说明闭合三角结构嵌入在专利技术扩散中发挥重要影响。
通过模型拟合优度GOF可以检验模型对专利技术扩散机制的捕捉能力。拟合优度分析的基本思路为:通过拟合模型进行网络仿真,根据式(1)给出的随机网络概率分布,采用MCMC法进行网络采样,如果得到的模拟网络与原网络具有相似的结构特征,则说明模型拟合效果好,能够很好地还原原网络。结构特征有多种指标,本文选取典型指标——边共享伙伴EP(i)(edge-wise share partners)。图2给出了模型1-4的拟合优度比较,其中,纵轴代表网络边的对数几率,横轴代表构型-边共享伙伴EP(i),箱型代表模拟网络特征,黑实线代表原网络特征。比较4个子图可以发现,模型1(左上角)和模型2(右上角)高估了指标EP(0),但低估了指标EP(1)、EP(2)。另外,整体上,模型3(左下角)和模型4(右下角)具有相近的网络还原能力,而在指标EP(2)处,模型4的表现略好于模型3。总体上,模型4的拟合优度最佳,且AIC和BIC指标值也最小,说明模型4最准确地捕捉了专利技术扩散网络形成机制。
表3 ERGM模型参数估计结果

模型1模型2模型3模型4Nodeicov(tc)0.110(0.003)***0.088(0.004)***Nodeicov(width)-0.215(0.019)***-0.110(0.015)***Homo(cy)0.563(0.084)***0.495(0.088)***Homo(ass)1.113(0.099)***1.161(0.101)***Homo(ipc)0.994(0.077)***1.213(0.084)***Dgwdsp-1.764(0.105)***-1.575(0.105)***Dgwesp4.145(0.232)***2.616(0.255)***Edeges-5.961(0.059)***-7.140(0.072)***-5.143(0.047)***-5.981(0.091)***AIC10 18710 4459 9388 995BIC10 21910 4899 9709 083
注:括号中为参数估计量的标准差;***代表p<0.001
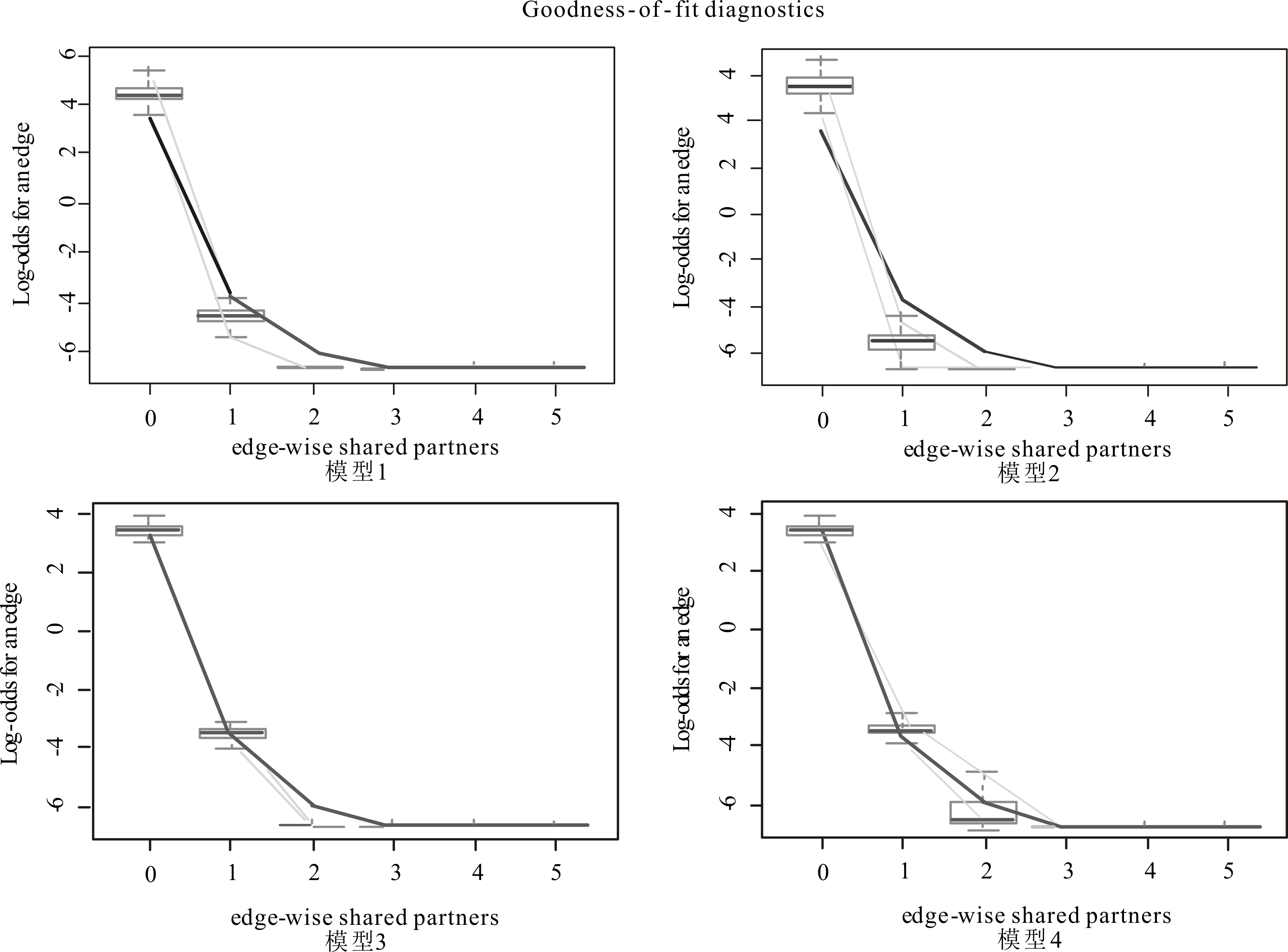
图2 模型拟合优度GOF比较
4 结语
将专利技术扩散因素归纳为4个方面:专利价值、专利保护、多维同配、结构嵌入。同时,将因素变量划分为网络外生、内生变量,采用指数随机图模型进行实证。以石墨烯领域专利为样本,实证研究得到以下基本结论:专利价值、专利保护分别促进、抑制技术扩散;多维同配方面,技术、地理、组织层面的同配促进了专利技术扩散;结构嵌入方面,专利技术扩散倾向于嵌入三角闭合结构。进一步,研究得到如下启示:
(1)应充分重视专利保护的负面效应。专利制度从诞生之日起就存在不断的争议,实证结果说明,专利保护对技术扩散存在抑制作用,更进一步验证了专利制度的双面性。事实上,专利保护的本质在于将部分市场无法自动调节的社会收益强制性地转化为私人收益,在外部收益内化的过程中,必然导致社会福利减少、私人收益增加。因此,专利保护水平是个体利益与社会福利之间的平衡,关键问题在于如何实现不同情境下最优制度设计与实践。已有文献指出,理论上最优专利保护可能存在国家、行业的差异,因此实践中需要充分考虑影响专利制度效果的权变因素。这一点对于处于转型发展期的我国具有重要启示:①应根据我国国情制定适宜的专利保护政策,过度的专利保护反而不利于我国技术追赶与进步;②不应过度夸大或贬低专利制度的复杂多元创新效应,而应开展顶层制度设计,在激励技术创新主体的同时,保障技术扩散的社会福利最大化。
(2)技术、地理、组织的接近性促进技术扩散。多维同配现象反映出技术扩散是技术与社会系统共同作用的结果。实证说明,技术知识流动、溢出受到各种有形或无形边界的约束,集中于特定技术领域内,更受到地理空间、组织关系的影响,其中组织边界的抑制效应最显著。多维同配反映了技术知识的社会环境嵌入性,尤其是隐性知识根植于创新个体、特定组织及局部空间,难以简单复制和低成本转移。研究启示在于:政府及企业应该设法降低跨界性技术扩散门槛,例如为科研人员构建便捷、稳定、高效的合作交流平台,提高创新要素的空间集聚性,促进多学科技术领域的融合创新。
(3)结构嵌入是深入认知专利技术扩散复杂性的重要视角。实证结果说明,结构嵌入对专利技术扩散的影响稳定而强烈,其影响程度远超预期。该结论的启示在于:专利技术扩散网络复杂性是深入认知其背后机制的重要基础,而刻画网络边自相关性可能是揭示专利技术扩散内在动力的重要视角。指数随机图模型具有捕捉结构效应的能力,能够为深入揭示专利技术扩散内在动力机制提供有力支持。
本文贡献在于从网络内生因素、外生因素两个层面分析专利技术扩散机制,并采用指数随机图模型实证验证了专利技术扩散机制。相比已有多数文献对结构嵌入效应的忽略,本文分析模型更全面,结论相对可靠。此外,石墨烯是典型新兴技术,后续研究有必要选择相对成熟的技术领域作为实证对象,以检验本结论的普适性。
[1] SOMAYA D.Patent strategy and management: an integrative review and research agenda[J].Journal of Management, 2012, 38(4): 1084-1114.
[2] MANSFIELD E, SCHWARTZ M, WAGNER S.Imitation costs and patents: an empirical study[J].Economic Journal, 1981, 91(364): 907-918.
[3] JAFFE A, TRAJTENBERG M, HENDERSON R.Geography, location of knowledge spillovers as evidence of patent citations[J].Quarterly Journal of Economics, 1993, 108(3): 577-598.
[4] 吕永卫, 周瑞敏.基于企业网络组织的技术创新扩散过程分析[J].山西农业大学学报:社会科学版, 2011, 10(10): 984-989.
[5] 孙冰, 赵健.知识密集型产业技术创新扩散演化研究——基于网络结构演化分析的视角[J].情报杂志, 2013(1): 198-203.
[6] 孙德忠, 周荣, 喻登科.高校与非高校上市公司专利技术扩散网络模型[J].科学学与科学技术管理, 2014(1): 57-65.
[7] 叶建木, 马玎, 张雅蕊.垃圾发电技术专利合作网络的动态演化分析[J].武汉理工大学学报:社会科学版, 2017, 30(2): 32-38.
[8] PENG T Q.Assortative mixing, preferential attachment, and triadic closure: a longitudinal study of tie-generative mechanisms in journal citation networks[J].Journal of Informetrics, 2015, 9(2): 250-262.
[9] 郭磊, 蔡虹, 张越.专利战略化情境下的产业核心专利态势分析[J].科学学研究, 2016, 34(11): 1663-1671.
[10] 张鹏, 李新春.专利制度与技术创新之间关系的思考[J].自然辩证法研究, 2002, 18(6): 72-73.
[11] ARROW K J.Economic welfare and the allocation of resources for invention[M].London: Macmillan Education UK, 2009.
[12] 饶睿.专利制度对技术创新扩散的负效应研究[J].科技管理研究, 2009, 29(5): 398-400.
[13] CHANG S B, LAI K K, CHANG S M.Exploring technology diffusion and classification of business methods: using the patent citation network[J].Technological Forecasting & Social Change, 2009, 76(1): 107-117.
[14] NARIN F, HAMILTON K S, OLIVASTRO D.The increasing linkage between U.S.technology and public science[J].Research Policy, 1997, 26(3): 317-330.
[15] SHIH H Y, CHANG T.International diffusion of embodied and disembodied technology: a network analysis approach[J].Technological Forecasting & Social Change, 2009, 76(6): 821-834.
[16] JAFFE A B, TRAJTENBERG M, HENDERSON R.Geographic localization of knowledge spillovers as evidenced by patent citations[J].Quarterly Journal of Economics, 1993, 108(3): 577-598.
[17] 任胜钢, 吴娟, 王龙伟.网络嵌入结构对企业创新行为影响的实证研究[J].管理工程学报, 2011, 25(4): 75-80.
[18] 高良谋, 马文甲.开放式创新:内涵、框架与中国情境[J].管理世界, 2014(6): 157-169.
[19] GOODREAU S M.Advances in exponential random graph (p*) models applied to a large social network[J].Social Networks, 2007, 29(2): 231-248.
[20] SNIJDERS T A B, PATTISON P E, ROBINS G L, et al.New specifications for exponential random graph models[J].Sociological Methodology, 2006, 36(1): 99-153.
[21] ROBINS G, PATTISON P, KALISH Y, et al.An introduction to exponential random graph (p*) models for social networks[J].Social Networks, 2007, 29(2): 173-191.