
图1 重大突发事件上级政府-地方分工决策模式
摘 要:针对大型工程项目突发事件应急决策参与者权利分布导致的风险,提出了一种大群体风险应急决策方法。首先,利用信息熵理论,提出了一种测量大群体决策风险的测度模型;其次,对参与决策的大群体在决策过程中由于权利分布引起的风险进行了定量计算;然后,利用风险大小确定最终偏好信息的集结结果,对应急方案进行排序选优。最后,通过工程项目建设中仓库爆炸突发事件案例分析,验证了该方法的有效性。
关键词:工程建设;突发事件;权利分布;风险测度;大群体应急决策
大型工程项目突发事件一般指在一定时间、地域内意外发生的对工程建设、生命和财产造成重大损失的事件[1],如天津港“8·12”特大火灾爆炸事故等。简单来说,风险是指发生不利事件的可能性,在对重大突发事件的风险研究中,一般侧重于考虑事件现场应急处置行为可能导致的风险。根据前景理论[2]和后悔理论[3]等,考虑心理因素对风险决策的影响,以及个人偏好对选择结果的影响,本文考虑大群体决策中由于多重复杂偏好产生的风险。重大事件的决策者主要是政府,这种风险类似于政府决策风险。周斌[4]从决策参与者的角度分析政府投资项目决策风险管理,确定决策风险因素,并运用模糊聚类方法比较各风险因素的相关性,建立了政府投资项目决策参与者风险评价模型。由于复杂偏好的存在,决策者之间的偏好很可能存在较大冲突,这种冲突也是风险来源之一。徐选华[5]提出的偏好冲突优化的多属性多阶段大群体决策方法对决策者偏好进行了多阶段修正,对冲突进行优化,使风险降低。陈占锋[6]提出设置反方制度,从宏观体制层面设置极端化冲突方案,让决策者在互相讨论中得到一致结果。不同决策参与者给出的决策值形式可能是不同的,Fasolo[7]研究了数值和语言两种不同表达形式在决策中的不同表现以及对决策结果的影响,而实际决策中使用不同决策值形式也可能产生风险。
显然,对于大型工程项目中重大突发事件的决策,决策参与者复杂偏好导致的风险是多方面的,一般包括决策流程科学性、决策主体责任明确性、决策权力分配合理性、专家结构合理性、决策者业务水平、决策者社会责任感、决策者评价值表现形式、决策者人员动态变化、决策偏好引起的冲突以及决策者间人际交往等。为了控制诸多风险的不利影响,需要辅助工具对其进行测度和评估。以往的风险测度研究多针对金融领域[15-16,18,20],投资组合获得的收益可以直接用数值表示,代入测度模型定量计算风险进行风险控制。对于突发事件应急处置、投资项目、选址决策等情况,多是对风险因素进行识别和分析,最后对整个决策过程的风险进行评级与管理[10]。近年来,金融风险测度理论研究逐渐成熟,其它行业也渐渐开始对风险测度进行研究[17]。本文针对决策权利分布导致的风险,根据信息熵理论中对不确定性程度的定量计算[11,19],提出一种大群体决策风险度量方法。
在建大型工程重大突发事件应急决策过程具有时间压力大、影响广等特点,本文基于“7·23”甬温线特大铁路交通事故[8]、天津港“8·12”特大火灾爆炸事故[9]以及其它近年来特大突发事故的应急处置资料,在现有应急决策与风险测度研究成果的基础上,基于风险测度,提出一种新的面向大型工程项目建设过程中重大突发事件的大群体应急决策方法。
1.1 问题描述
根据相关重大突发事件调查报告中的应急处置资料[8-9],可以得出重大突发事件应急决策主要包括3个方面:①阻止现场情况恶化方案的快速选择,如压制事件、疏散人群等,主要是当地政府相关部门直接进行应急决策,决策时间非常短,对动态决策能力要求很高;②现场救援方案选择,不同事件现场出现的紧急情况可能不同,一般来说,当地政府都有应急预案供选择;③选择医疗救治以及善后工作方案,对医疗资源调度以及救助补偿等事项进行决策。近年来,随着信息化的普及,网络舆情[12]也成为重大突发事件应急决策需要重视的一环,文献[8]中提及媒体报道不完全导致公众误以为救援停止的情况,舆情处理不及时会影响现场救援行动,针对网络舆情,主要是实时监测,发现异常后通过官方媒体公布方案选择。
决策过程中,一般由上级领导召开会议听取现场情况报告,并作出批示,当地成立事故救援处置总指挥部,统筹组织相关部门力量、调取各地专家进行实地救援方案决策。上级政府会与地方指挥部进行电话或者视频等直接联系,也会派遣上级政府领导亲临现场进行监督指导,会对地方决策产生影响。上级政府决策者对地方参与决策的专家背景资料了解详细,地方决策的专家团队则对现场实际情况更为清楚。由此可建立上级-地方分工决策模式,如图1所示。
假设上级决策者决定参与地方决策的总人数为m,并在集结决策信息的过程中决定每个地方参与决策者的权重范围区间,决策者权重之和为1,不断尝试计算风险最小时的权重分配,集结偏好信息对方案进行排序。

图1 重大突发事件上级政府-地方分工决策模式
针对大型工程项目重大突发事件的大群体决策问题,基本符号规定如下:
Ω={e1,e2,…,ei,…,em},表示m个地方决策参与者的集合,其中,m>20[21];
A={a1,a2,…,al,…,ap},表示重大突发事件p个备选应急预案的集合;
C={c1,c2,…,cj,…,cn},表示应急方案n个属性的集合;
W=(w1,w2,…,wn)T,表示属性权重向量,满足![]()
ω=(ω1,ω2,…,ωm)T,表示决策群体内决策者的权重向量。
1.2 决策参与者权利分布风险测度
大型工程项目建设过程中重大突发事件应急决策参与者权利分布导致的风险,主要是指在集结所有参与者意见时各种因素导致决策结果不能充分表达多数人意愿的情况。
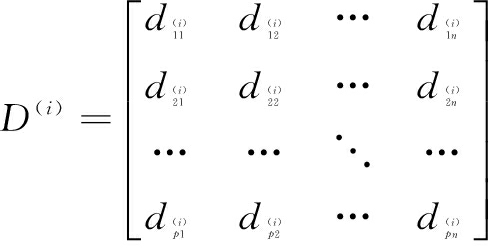
设决策群体第i个成员关于第l个方案的第j个属性的评价值为![]() 则m个成员各自给出的偏好矩阵如下:
则m个成员各自给出的偏好矩阵如下:

采用信息熵方法对整个决策群体在集结过程中的风险进行测度,已知方案的属性权重向量W和成员权重ω。
(1)对于第j个属性的所有评价值![]() 将[0,1]区间平均分为h个小区间,h的大小由决策者给出,则第s个小区间为
将[0,1]区间平均分为h个小区间,h的大小由决策者给出,则第s个小区间为![]() 根据成员权重可得评价值
根据成员权重可得评价值![]() 落在第s个小区间的概率:
落在第s个小区间的概率:
(1)
(2)本文采用信息熵表示集结评价信息的平均不确定程度,计算所有方案的第j个属性评价值在集结过程中因为权利分布产生的风险:
(2)
可得到风险向量:
E=(E1,E2,…,En)T
(3)求得此时决策参与者由于权利分布不均导致的风险熵值:
R=WT·E
(3)
1.3 决策步骤
第一步:地方指挥中心将现场情况汇报给上级政府,上级决策者决定参与决策的各部门专家名单(m>20个),构成决策大群体Ω,并给出备选方案的所有属性C以及属性权重W。
第二步:地方决策者根据上级政府给出的信息,召集上述人员及时参与决策,已知第i个成员关于第l个方案的第j个属性的评价值为![]() 则可得到m个偏好矩阵:
则可得到m个偏好矩阵:
根据文献[13]中相聚度计算公式,可得第i1个成员与第i2个成员关于第j个属性的偏好相聚度:
(4)
其中,||·||2指向量的二范数。第i1个成员与第i2个成员的偏好相聚度为:
(5)
对成员随机排序,选取第一个成员组成聚集Ω1,将其与剩下成员两两计算偏好相聚度,确定合适的阈值γ,相聚度结果大于该阈值的成员加入Ω1。找到所有加入Ω1的成员后按顺序选取剩下成员中序号最前者,继续与其他没有加入聚集Ω1的成员两两计算偏好相聚度,与阈值γ对比,大于该阈值则一起组成第二个聚集Ω2。当某一决策者与其余决策者的偏好相聚度都低于阈值γ时,令其单独成为一个聚集。由此循环,直到所有决策者都加入相应的聚集为止。设此时决策群体被聚类为K个聚集,即![]()
第三步:将上一步结果返回给上级政府,由上级决策者给出统一标准下各聚集内每个专家的权重区间。对于![]() 中任一聚集Ωk(其成员数记为nk),给出Ωk成员权重区间的下确界集
中任一聚集Ωk(其成员数记为nk),给出Ωk成员权重区间的下确界集![]() 与上确界集
与上确界集![]()
∀
可随机取得Ωk中成员的权重![]() 并满足如下条件:①
并满足如下条件:①![]() ②
②![]()
由上级决策者给出每个聚集整体的权重区间下确界集Inf={a1,a2,…,ag,…,aK}以及上确界集Sup={b1,b2,…bg,…,bK},其中,∀ag∈[0,1),bg∈(0,1]且![]() 将各聚集内信息分别集结成代表各自聚集的一个决策矩阵,集结代表各聚集决策信息时的聚集权重在所给区间内随机选取,即ωg∈[ag,bg],g=1,2,…,K,并满足
将各聚集内信息分别集结成代表各自聚集的一个决策矩阵,集结代表各聚集决策信息时的聚集权重在所给区间内随机选取,即ωg∈[ag,bg],g=1,2,…,K,并满足![]()
第四步:根据决策大群体聚类结果![]() 对每个聚集内专家权重进行计算。对于任一聚集Ωk,给出一组随机数
对每个聚集内专家权重进行计算。对于任一聚集Ωk,给出一组随机数![]() ∀
∀![]() 根据聚集相应的权重区间上、下确界集,令
根据聚集相应的权重区间上、下确界集,令![]() 得到向量Y={y1,y2,…,ynk},对Y进行归一化后得到
得到向量Y={y1,y2,…,ynk},对Y进行归一化后得到![]() 此时显然满足条件②。判断ωk是否满足条件①,若不满足则重新选取随机数,继续寻找符合两个条件的专家权重向量;若满足,即可将ωk作为一个专家权重向量。当得到一个符合要求的ωk时,即可根据本文提出的决策参与者权力分布风险测度模型,计算在此权重分配下该聚集的权利分布风险。
此时显然满足条件②。判断ωk是否满足条件①,若不满足则重新选取随机数,继续寻找符合两个条件的专家权重向量;若满足,即可将ωk作为一个专家权重向量。当得到一个符合要求的ωk时,即可根据本文提出的决策参与者权力分布风险测度模型,计算在此权重分配下该聚集的权利分布风险。
聚集Ωk针对l个方案n个属性的决策矩阵如下:
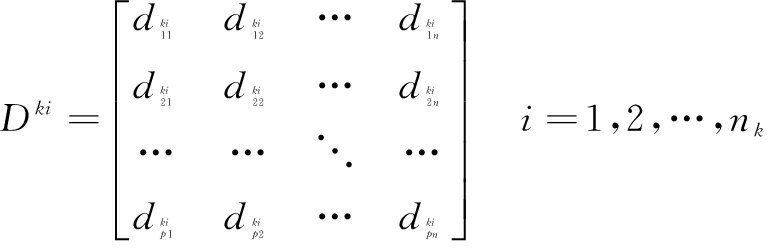
已知Ωk内成员关于第l个方案的第j个属性的评价值![]() 根据式(1)计算其落在不同区间的概率分布,再根据式(2)计算上述分布在集结信息过程中产生的风险,最后根据式(3)计算该聚集集结信息的总风险熵值。
根据式(1)计算其落在不同区间的概率分布,再根据式(2)计算上述分布在集结信息过程中产生的风险,最后根据式(3)计算该聚集集结信息的总风险熵值。
重复选取随机数适当次数,得到多组专家权重向量,按照上述过程依次计算每组的风险熵值,选取风险熵值最小时对应的最佳权重向量![]() 运用加权平均算子[14]集结聚集Ωk内的决策信息,得到
运用加权平均算子[14]集结聚集Ωk内的决策信息,得到![]() 运用以上方法对每一个聚集进行处理,得到每个聚集风险熵值都取到最小值时的集结结果,即得到相当于聚集数量K的决策偏好矩阵。
运用以上方法对每一个聚集进行处理,得到每个聚集风险熵值都取到最小值时的集结结果,即得到相当于聚集数量K的决策偏好矩阵。
第五步:在所给每个聚集的权重区间分别选取一个随机数进行组合,再对每组随机数进行归一化处理,选取多个满足限制区间的权重组合,依次对集结过程进行风险度量,选择风险最小时的集结结果![]() 即得到一个集结所有聚集信息的决策偏好矩阵
即得到一个集结所有聚集信息的决策偏好矩阵![]() 最终根据已给属性权重W,计算所有方案的最终得分F=WT·D,并对其按大小排序,返回上级决策者,审批通过即可安排实施。
最终根据已给属性权重W,计算所有方案的最终得分F=WT·D,并对其按大小排序,返回上级决策者,审批通过即可安排实施。
某大型建筑工程项目工地材料仓库突发重大火灾,附近公安局110指挥中心接到报警电话后迅速调集附近消防队进行现场灭火以及人群疏散,由于火势蔓延迅速并引起爆炸,伤亡人数与财产损失不断增加,达到特大灾害等级,指挥中心当即联系上级政府,汇报现场细节情况。
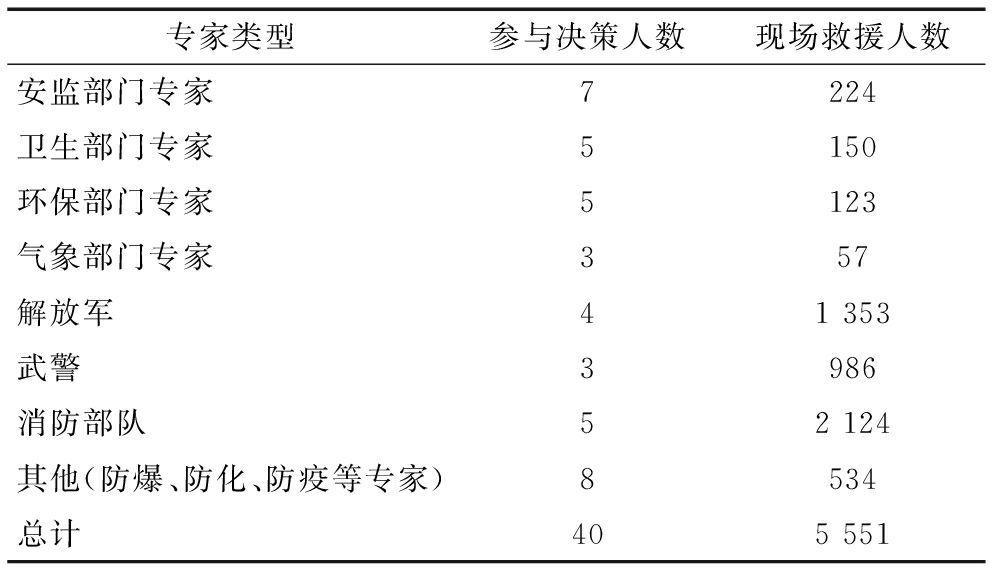
第一步:上级政府成立4人决策小组,由组内最高级别领导人带领对本次特大突发事件进行决策,调度各相关部门人员前往现场进行救援和决策指导,如表1所示。
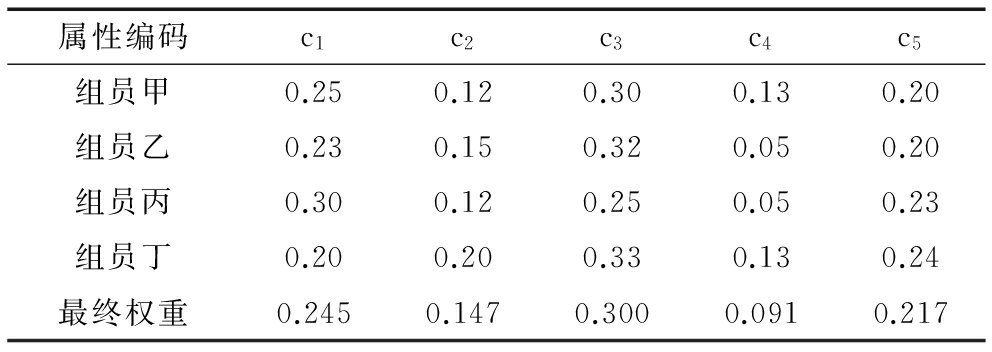
对于已知4条不同的人群疏散路线A={a1,a2,a3,a4},上级决策小组根据现场反馈的信息给出了5种需要列入参考的属性,C={c1,c2,c3,c4,c5}。其中,c1表示路过地形方便程度,c2表示当地天气适宜程度,c3表示附近医疗设施完备程度,c4表示附近不发生次生灾害的可能程度,c5表示附近物资充足程度。上级小组每个成员给出属性权重建议值再取平均值,得出方案的每个属性权重W={w1,w2,w3,w4,w5},如表2所示。上级决策小组给出了40位决策者,构建决策大群体Ω(={e1,e2,…,e40}。
表1 决策人员调度方案
专家类型参与决策人数现场救援人数安监部门专家7224卫生部门专家5150环保部门专家5123气象部门专家357解放军41353武警3986消防部队52124其他(防爆、防化、防疫等专家)8534总计405551
表2 方案属性权重分配
属性编码c1c2c3c4c5组员甲0.250.120.300.130.20组员乙0.230.150.320.050.20组员丙0.300.120.250.050.23组员丁0.200.200.330.130.24最终权重0.2450.1470.3000.0910.217
第二步:收到上级政府的通知,地方指挥部紧急联系决策参与群体,根据现场情况让他们对4个应急方案的5种属性分别进行快速评价,限于篇幅,评价结果省略。运用相聚度公式[13]计算决策偏好矩阵之间相聚度,并将相聚度在所给阈值γ=0.8[13]以上的决策者进行聚类,这里以两个决策者e1和e2决策矩阵之间的相聚度计算为例(利用Mallab编程计算)。已知两者的决策矩阵如下:


分别计算决策者e1、e2关于每个属性的偏好相聚度:
j=1,2,…5
计算结果如表3所示。
表3 决策者e1和e2关于各属性的相聚度情况
属性编号c1c2c3c4c5相聚度0.80860.97710.368410.9349
根据上级决策者给出的属性权重分配可求得二者的总相聚度:
r12=0.245×0.808 6+0.147×0.977 1+0.301
×0.368 4+0.091×1+0.216×0.934 9=0.745 6
当γ=0.8时,对两两决策者计算相聚度并将相聚度大于0.8的决策者进行聚类,结果如表4所示。
第三步:将以上所得结果返回给上级决策小组,分别考虑上级决策者决定划分区间数目h=5和h=10的情况,并给出每个聚集内各位专家的权重区间,要求保证聚集内所有成员在所给区间内权重之和为1。限于篇幅,所给区间数省略。上级决策小组根据人数为每个聚集赋予权重区间,如表5所示。
表4 决策者聚类结果

聚集成员数成员聚集一致性指标Ω111e1,e5,e10,e12,e13,e22,e31,e32,e36,e37,e380.8521Ω25e2,e9,e18,e21,e250.8925Ω37e3,e7,e11,e17,e27,e30,e350.9335Ω48e4,e15,e19,e28,e33,e34,e39,e400.9290Ω55e6,e14,e20,e23,e240.8539Ω64e8,e16,e26,e290.9486
第四步:多次随机选取所给区间中的数,归一化形成满足条件的每个决策者的权重,对此权重分配下的集结风险进行度量,选择10次有效的风险熵结果进行对比,取风险熵最小权重分配结果进行集结。可以得到每个聚集的最佳权重分配,如表6、表7所示,利用Mallab编程计算得到每个聚集的集结结果,如表8、表9所示。
表5 聚集权重区间情况
聚集编号Ω1Ω2Ω3Ω4Ω5Ω6权重区间[0.3,0.4][0.1,0.2][0.2,0.3][0.2,0.3][0,0.1][0,0.1]
第五步:从表5中权重区间内选取随机数,保证归一化后得到的权重都在所给权重区间内,进行10次以上有效操作,计算集结风险,结果如表10与表11所示。本文选择风险最小的一组权重分配,即h=5时选择ω*=(0.3704,0.1017,0.2125,0.2924,0.0055,0.0175)T以及h=10时选择ω*=(0.3249,0.1702,0.2227,0.2576,0.0145,0.0101)T,集结可得到最终决策评价值,并根据表2中属性权重,计算得到每个方案的最终评价值,结果如表12、表13所示。
最终确定两种情况下应急方案排序结果都为:a1 >a2 >a3 >a4,将以上结果交给上级决策小组,决定最终应急方案。
表6 h=5时每个聚集的最佳权重分配

聚集权重向量风险值Ω1(0.0912,0.0730,0.0311,0.0745,0.0880,0.0981,0.0984,0.0950,0.0655,0.0981,0.1872)T0.5070Ω2(0.5576,0.1075,0.1976,0.0601,0.0772)T0.2368Ω3(0.0881,0.0681,0.0938,0.0227,0.1251,0.2974,0.3047)T0.9813Ω4(0.2456,0.0052,0.1706,0.1188,0.3008,0.0123,0.0115,0.1352)T0.5000Ω5(0.1371,0.0493,0.5811,0.0293,0.2033)T0.5215Ω6(0.0787,0.8617,0.0181,0.0415)T0.0702
表7 h=10时每个聚集的最佳权重分配

聚集权重向量风险值Ω1(0.0887,0.0921,0.0847,0.0500,0.0776,0.0980,0.0972,0.0502,0.0987,0.0735,0.1894)T0.5708Ω2(0.5520,0.1010,0.1273,0.0386,0.1811)T0.7886Ω3(0.0294,0.0889,0.0616,0.0821,0.1795,0.2150,0.3434)T0.7008Ω4(0.2106,0.0032,0.1252,0.1849,0.3019,0.0271,0.0322,0.1148)T0.6441Ω5(0.1051,0.0085,0.5161,0.1004,0.2699)T0.8766Ω6(0.0614,0.8270,0.0452,0.0664)T0.1656
表8 h=5时各聚集集结信息后的结果
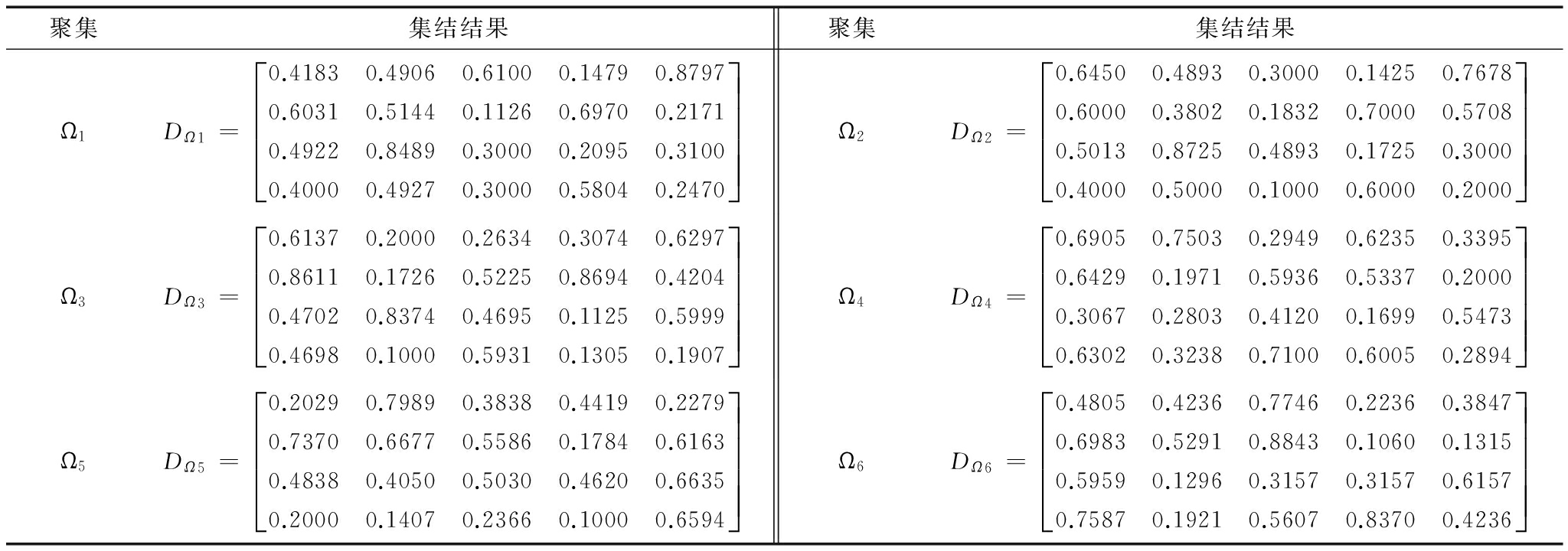
聚集集结结果聚集集结结果Ω1DΩ1=0.4183 0.4906 0.6100 0.1479 0.87970.6031 0.5144 0.1126 0.6970 0.21710.4922 0.8489 0.3000 0.2095 0.31000.4000 0.4927 0.3000 0.5804 0.2470éëêêêêùûúúúúΩ2DΩ2=0.6450 0.4893 0.3000 0.1425 0.76780.6000 0.3802 0.1832 0.7000 0.57080.5013 0.8725 0.4893 0.1725 0.30000.4000 0.5000 0.1000 0.6000 0.2000éëêêêêùûúúúúΩ3DΩ3=0.6137 0.2000 0.2634 0.3074 0.62970.8611 0.1726 0.5225 0.8694 0.42040.4702 0.8374 0.4695 0.1125 0.59990.4698 0.1000 0.5931 0.1305 0.1907éëêêêêùûúúúúΩ4DΩ4=0.6905 0.7503 0.2949 0.6235 0.33950.6429 0.1971 0.5936 0.5337 0.20000.3067 0.2803 0.4120 0.1699 0.54730.6302 0.3238 0.7100 0.6005 0.2894éëêêêêùûúúúúΩ5DΩ5=0.2029 0.7989 0.3838 0.4419 0.22790.7370 0.6677 0.5586 0.1784 0.61630.4838 0.4050 0.5030 0.4620 0.66350.2000 0.1407 0.2366 0.1000 0.6594éëêêêêùûúúúúΩ6DΩ6=0.4805 0.4236 0.7746 0.2236 0.38470.6983 0.5291 0.8843 0.1060 0.13150.5959 0.1296 0.3157 0.3157 0.61570.7587 0.1921 0.5607 0.8370 0.4236éëêêêêùûúúúú
表9 h=10时各聚集集结信息后的结果
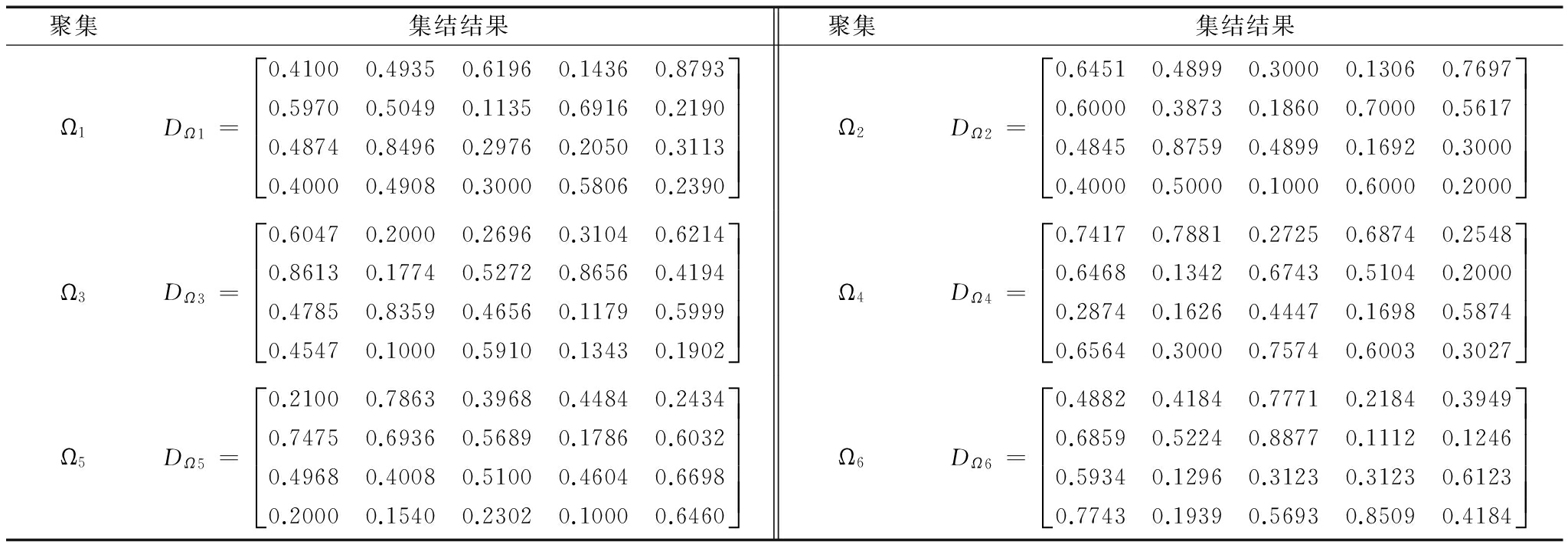
聚集集结结果聚集集结结果Ω1DΩ1=0.4100 0.4935 0.6196 0.1436 0.87930.5970 0.5049 0.1135 0.6916 0.21900.4874 0.8496 0.2976 0.2050 0.31130.4000 0.4908 0.3000 0.5806 0.2390éëêêêêùûúúúúΩ2DΩ2=0.6451 0.4899 0.3000 0.1306 0.76970.6000 0.3873 0.1860 0.7000 0.56170.4845 0.8759 0.4899 0.1692 0.30000.4000 0.5000 0.1000 0.6000 0.2000éëêêêêùûúúúúΩ3DΩ3=0.6047 0.2000 0.2696 0.3104 0.62140.8613 0.1774 0.5272 0.8656 0.41940.4785 0.8359 0.4656 0.1179 0.59990.4547 0.1000 0.5910 0.1343 0.1902éëêêêêùûúúúúΩ4DΩ4=0.7417 0.7881 0.2725 0.6874 0.25480.6468 0.1342 0.6743 0.5104 0.20000.2874 0.1626 0.4447 0.1698 0.58740.6564 0.3000 0.7574 0.6003 0.3027éëêêêêùûúúúúΩ5DΩ5=0.2100 0.7863 0.3968 0.4484 0.24340.7475 0.6936 0.5689 0.1786 0.60320.4968 0.4008 0.5100 0.4604 0.66980.2000 0.1540 0.2302 0.1000 0.6460éëêêêêùûúúúúΩ6DΩ6=0.4882 0.4184 0.7771 0.2184 0.39490.6859 0.5224 0.8877 0.1112 0.12460.5934 0.1296 0.3123 0.3123 0.61230.7743 0.1939 0.5693 0.8509 0.4184éëêêêêùûúúúú
表10 h=5时每个聚集的权重分配及风险大小
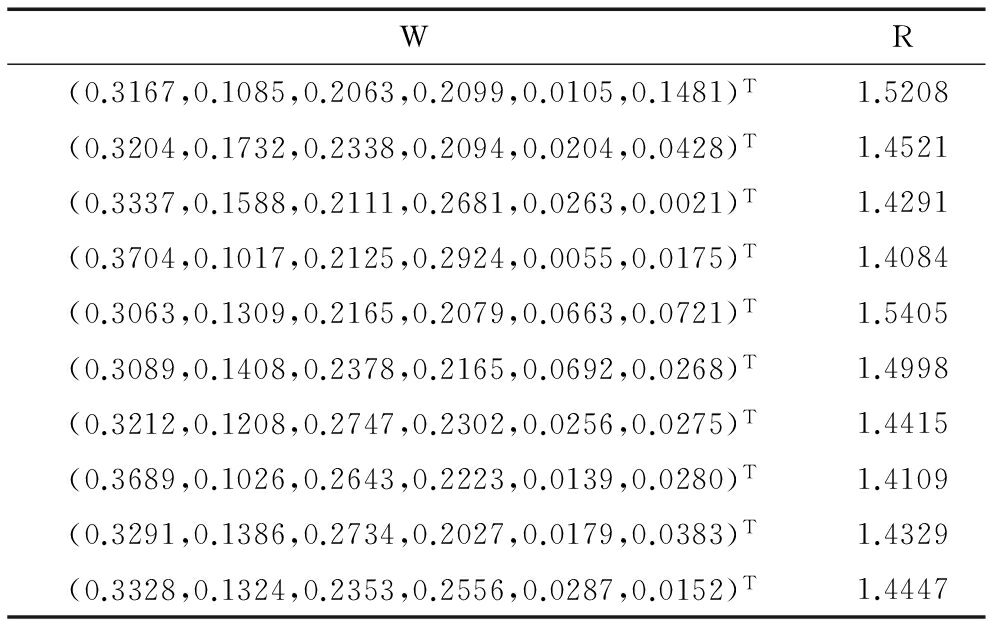
WR(0.3167,0.1085,0.2063,0.2099,0.0105,0.1481)T1.5208(0.3204,0.1732,0.2338,0.2094,0.0204,0.0428)T1.4521(0.3337,0.1588,0.2111,0.2681,0.0263,0.0021)T1.4291(0.3704,0.1017,0.2125,0.2924,0.0055,0.0175)T1.4084(0.3063,0.1309,0.2165,0.2079,0.0663,0.0721)T1.5405(0.3089,0.1408,0.2378,0.2165,0.0692,0.0268)T1.4998(0.3212,0.1208,0.2747,0.2302,0.0256,0.0275)T1.4415(0.3689,0.1026,0.2643,0.2223,0.0139,0.0280)T1.4109(0.3291,0.1386,0.2734,0.2027,0.0179,0.0383)T1.4329(0.3328,0.1324,0.2353,0.2556,0.0287,0.0152)T1.4447
表11 h=10时每个聚集的权重分配及风险大小
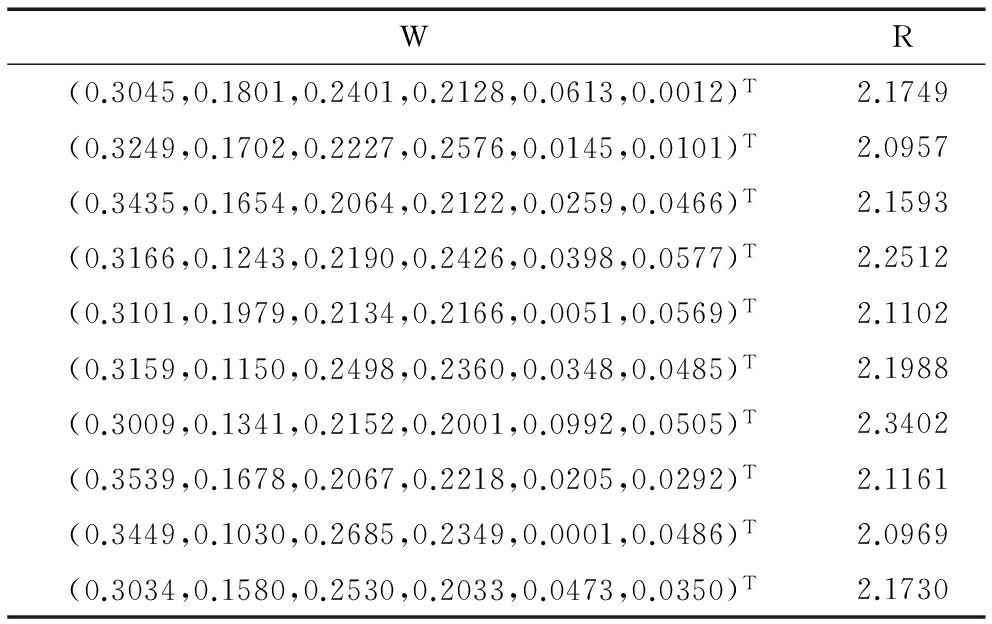
WR(0.3045,0.1801,0.2401,0.2128,0.0613,0.0012)T2.1749(0.3249,0.1702,0.2227,0.2576,0.0145,0.0101)T2.0957(0.3435,0.1654,0.2064,0.2122,0.0259,0.0466)T2.1593(0.3166,0.1243,0.2190,0.2426,0.0398,0.0577)T2.2512(0.3101,0.1979,0.2134,0.2166,0.0051,0.0569)T2.1102(0.3159,0.1150,0.2498,0.2360,0.0348,0.0485)T2.1988(0.3009,0.1341,0.2152,0.2001,0.0992,0.0505)T2.3402(0.3539,0.1678,0.2067,0.2218,0.0205,0.0292)T2.1161(0.3449,0.1030,0.2685,0.2349,0.0001,0.0486)T2.0969(0.3034,0.1580,0.2530,0.2033,0.0473,0.0350)T2.1730
本文提供了一种针对大型工程项目建设重大突发事件应急决策问题的大群体多属性风险决策方法,构建了风险测度方法计算决策风险,并化解集结过程中的风险,使结论更好地反映决策者意见。通过对偏好相聚度与决策者权利分布风险的计算,考虑决策者偏好差异以及权利分布共同作用下的风险。之所以选择给出区间进行随机计算,找到合适的权重,是因为人在处理海量信息时往往不能用一个精确的数字表示其全部意见,而给出模糊区间,可以让高速运转的计算机寻找到既符合决策者要求,又更好地体现多人意见的结果。实际上,在上级决策者方面,可以进一步拓展相关研究,结合大数据计算方法,选取更合适的人数和分配方案,并且实际参与决策的人数可以是动态变化的。本文提出的方法可以处理动态大群体情况,在此基础上也可围绕动态决策参与者的风险控制展开深入研究。
本文也存在一定局限性,比如当随机数的选取范围限制过多时,难以从随机数中找到完全符合条件的权重组合;当随机数选取范围限制较少时,风险大小变化剧烈。可以考虑采用数值逼近等方法,设置一个风险阈值,求解合适的权重区间,直到对应的风险值低于阈值。
表12 h=5时集结后的最终结果
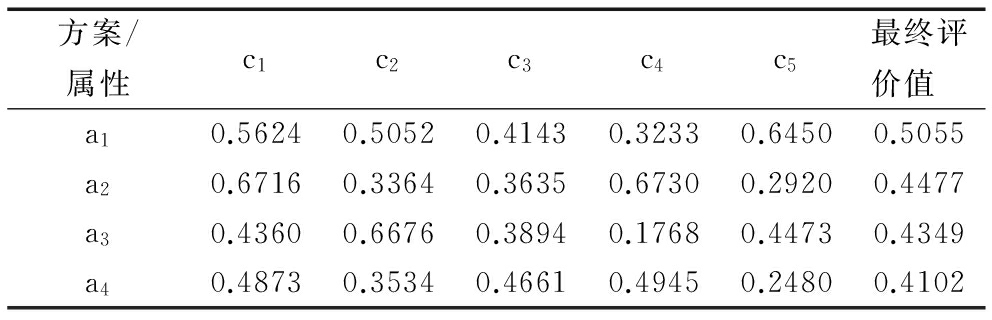
方案/属性c1c2c3c4c5最终评价值 a10.56240.50520.41430.32330.64500.5055a20.67160.33640.36350.67300.29200.4477a30.43600.66760.38940.17680.44730.4349a40.48730.35340.46610.49450.24800.4102
表13 h=10时集结后的最终结果
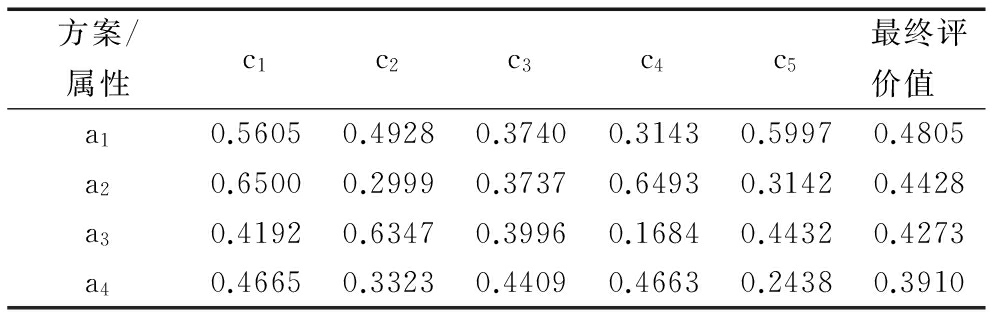
方案/属性c1c2c3c4c5最终评价值 a10.56050.49280.37400.31430.59970.4805a20.65000.29990.37370.64930.31420.4428a30.41920.63470.39960.16840.44320.4273a40.46650.33230.44090.46630.24380.3910
参考文献:
[1] 生产安全事故报告和调查处理条例[Z].中华人民共和国国务院令第493号,2007.
[2] DANIEL KAHNEMAN,AMOS TVERSKY.Prospect theory:an analysis of decision under risk[J].Econometrica,1979,47(2):263-291.
[3] BELL D E.Regret in decision making under uncertainty[J].Operations Research,1982,30(5):961-981.
[4] 周斌.政府投资项目决策参与者决策风险管理研究[D].杭州:浙江大学,2012.
[5] 徐选华,王敏赛,陈晓红.偏好冲突优化的多属性多阶段大群体决策方法[J].系统工程学报,2014,29(1):48-55.
[6] 陈占锋.加强和完善行政决策风险评估机制建设[J].行政管理改革,2012(9):70-74.
[7] FASOLO B,COSTA C A B E.Tailoring value elicitation to decision makers' numeracy and fluency:expressing value judgments in numbers or words[J].Omega,2014,44:83-90.
[8] “7·23”甬温线特别重大铁路交通事故调查报告[EB/OL].http://www.chinasafety.gov.cn/newpage/Contents/Channel_21679/2011/1228/244874/content_244874.htm.2011-10-11.
[9] 天津港“8·12”瑞海公司危险品仓库特别重大火灾爆炸事故调查报告[EB/OL].http://www.chinasafety.gov.cn/newpage/newfiles/201600812baogao.pdf.2016-10-11.
[10] AVEN T.Risk assessment and risk management:review of recent advances on their foundation[J].European Journal of Operational Research,2015,253(1):1-13.
[11] 张昕蕾.风险度量中的信息熵方法研究[D].北京:北京交通大学,2015.
[12] 肖文涛,范达超.网络舆情事件的引导策略探究[J].中国行政管理,2011(12):24-28.
[13] 徐选华,陈晓红,王红伟.一种面向效用值偏好信息的大群体决策方法[J].控制与决策,2009,24(3):440-445.
[14] YAGER R R,ALAJLAN N.Some issues on the OWA aggregation with importance weighted arguments[J].Knowledge-Based Systems,2016,100(C):89-96.
[15] 刘俊山.基于风险测度理论的证券投资组合优化研究[D].上海:复旦大学,2007.
[16] 郑承利,陈燕.基于等熵一致性风险测度的组合选择[J].系统工程理论与实践,2014(3):648-655.
[17] PENDER J,SLOWINSKI R,ARTALEJO J,et al.Risk measures and their application to staffing non-stationary service systems[J].European Journal of Operational Research,2016,254(1):113-126.
[18] YE W,LUO K,LIU X.Time-varying quantile association regression model with applications to financial contagion and VaR[J].European Journal of Operational Research,2017,256(3):1015-1028.
[19] FLEISCHHACKER A J,FOK P W.On the relationship between entropy,demand uncertainty,and expected loss[J].European Journal of Operational Research,2015,245(2):623-628.
[20] GRECHUK B,ZABARANKIN M.Inverse portfolio problem with coherent risk measures[J].European Journal of Operational Research,2015,249(2):740-750.
[21] LIU B,SHEN Y,CHEN X,et al.A complex multi-attribute large-group PLS decision-making method in the interval-valued intuitionistic fuzzy environment[J].Applied Mathematical Modelling,2014,38(17-18):4512-4527.
(责任编辑:万贤贤)
Large Group Emergency Decision Method of Major Emergencies for Engineering Construction Based on Right Distribution Risk Measure
Abstract:Aiming at the risk caused by the distribution of rights of decision-making participants of large engineering project, a large group risk emergency decision-making method is proposed. Firstly, a measure model for measuring the risk of large group decision-making is proposed by using information entropy theory. Secondly, the risk, which is derived from the distribution of rights when participating in the decision-making process, is quantitatively calculated. Then, the risk preference is used to determine the final preference information assembly. As a result, the emergency schemes are sorted accordingly. Finally, a case of warehouse explosion incident in construction project illustrates the effectiveness of the method.
Key Words:Engineering Construction; Emergencies; Right Distribution; Risk Measure; Large Group Emergency Decision
收稿日期:2017-04-01 基金项目:国家自然科学基金面上项目(71671189);国家自然科学基金重点项目(71431006);中南大学创新驱动计划项目(2015CX010)
DOI:10.6049/kjjbydc.2017GC0127
中图分类号:D630.8
文献标识码:A
文章编号:1001-7348(2017)09-0101-07