研发是技术创新最直接的来源，在科学技术日益综合化和复杂化的时代，企业研发所需要的知识存量和技术范围不断扩大，因此拥有有限资源的企业要提高创新能力，仅仅依赖于自身力量已无法满足技术创新要求。力求创新并获得更多利益，企业趋向于形成各种形式的合作联盟(例如创新联盟、生产者联盟等)，超越组织界限的企业间合作成为必然趋势。
企业合作联盟研究起源于20世纪80年代，其理论成果多以博弈论为基本研究工具，以寡头垄断产业为研究背景，分析和比较在存技术溢出情况下不同合作方式的研发水平、利润水平和社会福利水平等，从而筛选出更接近帕累托最优的竞合策略[1]。Kats[2]率先提出了合作研发并将其转化为多阶段的博弈过程。此后，Aspremont & Jacquemin[3](后文简称“AJ”)构建了合作研发博弈的标准分析框架，分析了技术溢出外生情况下，生产同质产品的企业在不同创新战略下研发投入水平和产量，研究证实如果溢出效应足够大，研发阶段的合作会激励企业加大研发投入，为通过博弈模型研究企业合作方式奠定了基础。鉴于双寡头假设的局限性，Suzumura[4]将其扩展为多寡头情形，在更一般条件下证实了AJ模型结论的可靠性。对AJ模型的另一个重要拓展来自Kamien等[5](后文简称“KMZ”)，他们从产品差异化和研发合作组织形式两个方面对AJ模型进行了扩展，在存在研发溢出情况下，比较了4种研发合作的组织方式，并证实在共同利润最大化目标驱动下，研发阶段合作且共享研发成果的研究联合体(RJV)是有利可图的。Ziss[6]则在存在溢出效应的两阶段博弈模型中，对完全竞争与局部合作(研发卡特尔)、价格安排(在价格或生产阶段合作)及完全合作(研发与生产阶段均合作)3种合作方式进行了比较，丰富并完善了KMZ模型。Kabiraj，Mukherjee[7]在KMZ模型基础上进一步构建了多寡头博弈模型，通过分析与对比RJV和研发卡特尔的研发绩效，发现RJV更有利于企业降低成本。另外，Atallah[8]从横向与纵向溢出率变化角度，研究了在不同组织模式下溢出效应对企业研发投入的影响，研究证实企业研发投入水平在纵向研发卡特尔中会更高。Ishii[9]，Stepanova等[10]则在Atallah基础之上证实AJ模型中的技术溢出属于产出溢出，该溢出效应有益于企业合作研发利润的提高，而KMZ模型中的溢出属于投入溢出，在投入溢出下垄断利润会更高。二者对比来看，产出溢出比投入溢出更利于降低企业成本[11]。总体来说，上述文献皆是基于溢出效应为[0,1]区间内某一定值的假设研究企业合作动机的。
在企业合作过程中，知识或技术外溢难以避免，并由此抑制了企业间相互合作的积极性。技术溢出按照溢出途径与形式可划分为租金溢出和纯知识溢出，前者与企业间的商品流动以及产品异质性有关，而后者则与专利信息、反向工程、科研人员跳槽等相关[12]。除AJ模型中的产出溢出与KMZ模型的投入溢出之外，Amir，Wooders[13]提出了从高强度研发企业流向其它企业的单向溢出，Hur，Watanabe[14]则进一步展示了单向溢出的动力学方法。单向溢出假设的提出虽贴近现实，但仍忽略了溢出效应与产品差异之间的紧密联系。为此，Piga&Poyago[15]将技术溢出与企业定价定位问题有机结合起来，其基本假设为溢出效应与企业间距离存在负相关关系。随后，Dey&Fu[16]在以Hotelling模型为代表的“线性空间模型”中，引入企业区位与技术溢出间的联系，并证实企业间差距越大，产品差异程度越大，技术溢出效应就越小。然而，此类文献均未涉及企业间的合作与竞争策略行为。
国内学者多从产业链上下游企业角度[17-20]和企业生命周期角度[21]研究溢出效应对企业研发活动及社会福利的影响。生延超[22]与游达明、朱桂菊[23]从政府介入技术联盟研发策略的方式出发，通过博弈模型分析了企业研发投入及政府补贴行为，研究证实企业研发投入会随着溢出效应的增强而增加。但斌等[24]从互补品的角度利用信号博弈模型研究了溢出效应对企业收益的刺激作用。茆训诚[25]和石光[26]则基于溢出效应和产品差异化双重视角，从动态角度考察了技术溢出对企业行为选择的影响。侯光明和艾凤义[27]以及苏素和肖阿妮[28]在同时考虑投入溢出和产出溢出的混合溢出情况下，利用合作研发博弈模型研究了双寡头的合作行为对研发成果、产量及利润的影响。张春辉和陈继祥[29]将溢出效应与研发投入的创新模式选择有机联系起来，并通过演化博弈理论对企业行为选择进行了分析，研究表明竞争企业溢出的增大会增加本企业选择颠覆性创新模式的概率。刘金平等[30]运用实验经济学方法，对存在溢出效应的企业合作研发模型的可靠度和有效性进行了检验，研究发现模型理论解与实验中的实际情况基本相符，溢出效应确能影响企业竞合行为。
本文借鉴Piga&Poyago-Theotoky的思路，认为溢出效应强度应与行业内产品差异以及企业间技术差距有关。与传统研究中对溢出效应的设定相比，“产品差异与技术差距影响研发溢出”的假设具有如下优势：首先，对于任意产品差异水平，该假设说明技术差距小的企业间溢出效应始终比技术差距大的企业间溢出效应强；其次，伴随产品差异的增大，溢出效应逐渐变弱，技术相近企业的溢出效应衰减速度为“先慢后快”，技术差异较大的企业间溢出效应衰减速度则为“先快后慢”。由上述两点可知，“产品差异与技术差距影响研发溢出”的假设能够更好地描述产品差异、技术差距与研发溢出三者间的关系，且更加贴近现实。基于此，本文通过构建双寡头企业研发与生产两阶段博弈模型，分析和比较不同形式合作联盟的均衡水平及福利变化，以期从微观角度对企业竞争与合作策略选择及各合作形式的稳定性进行深入探讨。
假定寡头垄断市场中有两个生产异质产品的企业。消费者效应函数为近似线性，具体如下：
(1)
其中，qi表示企业i的产出；a为常数且足够大，以保证每个企业的均衡产出均大于零；γ表示产品差异程度，该值越趋近于零，说明产品差异越大。根据式(1)可推导出企业i的反需求函数：
Pi(qi,qj)=a-qi-γqj
(2)
假设企业的生产边际成本为c，并且企业可通过增加研发投入来降低边际成本。由于研发过程中会存在溢出效应，因此企业的研发投入不仅会降低自身的生产边际成本，同时也会降低竞争对手的边际成本。假定企业j在研发上的投入为xj(j=1,2且i≠j)，则企业i的实际边际成本为Ci(xi,xj)=c-xi-βxj。由于研发投入的报酬递减特性，可认为研发成本是二次的，即
企业i的利润函数如下所示：
(3)
社会福利(W)为生产者剩余(PS)与消费者剩余(CS)之和，即：
W=PS+CS 其中PS=πi+πj;CS=U-piqi-pjqj
(4)
本文模型创新之处在于利用产品差异(γ)与技术差距(h)描述研发溢出的大小。令β为研发溢出效应，则：
β(γ,h)=γh 且h>0,γ∈[0,1)
(5)
为确保企业在所有合作形式中始终存在均衡，模型假定
越大，表示企业间的技术差距越大。当h<1时，说明企业采用相似技术来生产差异化的产品，例如苹果、华为、中兴等企业利用相似技术生产智能手机；如果手机产品间的差异越小，那么企业研发的溢出效应便会越大，此时研发溢出效应β与产品差异γ间呈“凹型”。而当h>1时，企业生产过程中所采用的技术存在较大差异，例如电力企业会通过转化太阳能、风能、核能等差异技术进行发电(电压存在差异，主要包括民用电220V、工业用电380V或更高电压电力)，此时研发溢出效应与产品差异间呈“凸型”(见图1)。
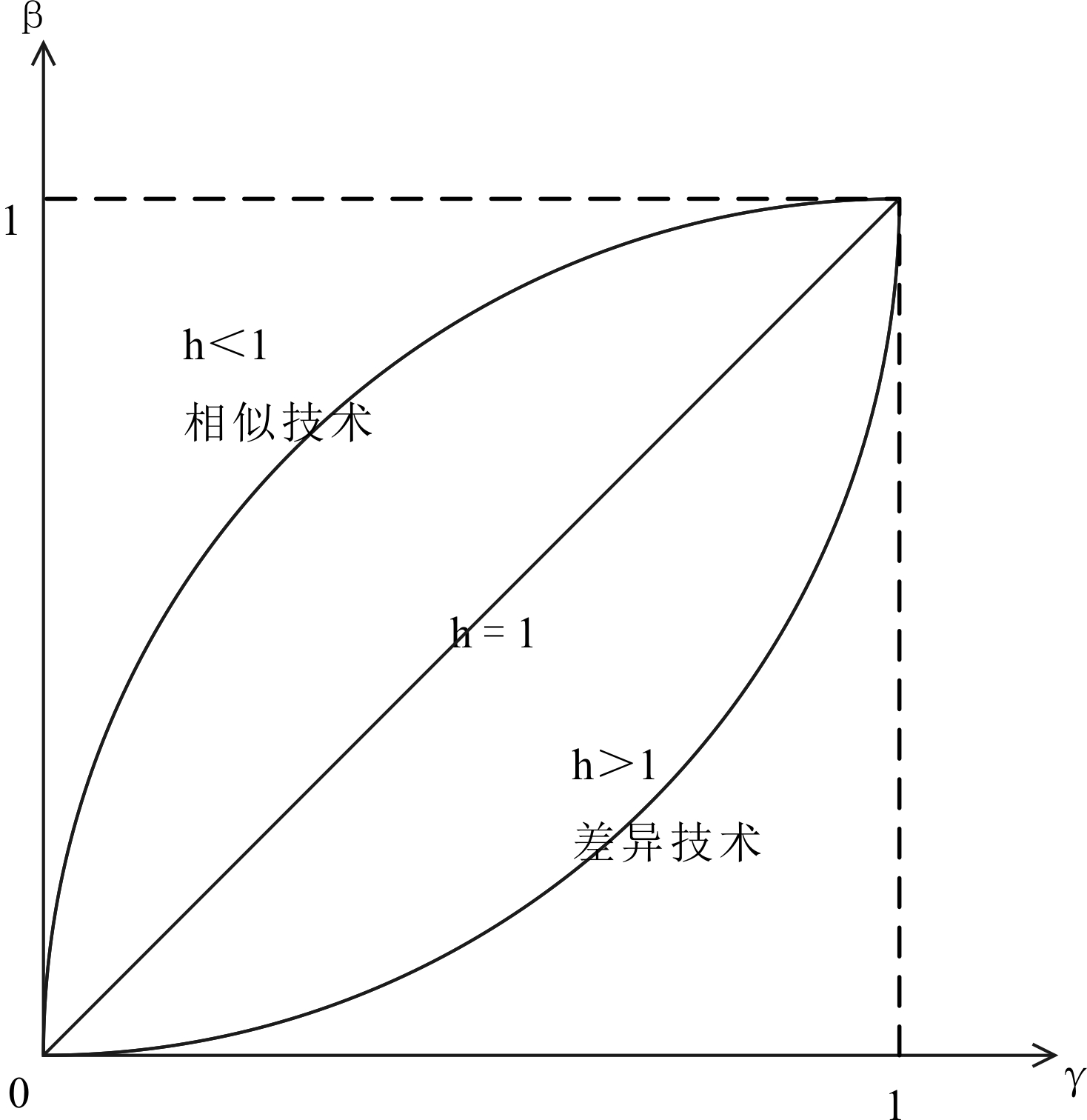
图1 研发溢出效应
此外，式(5)所描述的溢出效应还具有以下特性：首先，对于任意的产品差异水平，拥有相似技术企业之间的溢出效应始终比拥有差异技术企业间溢出效应要大；其次，伴随产品差异的增大(γ减小)，溢出效应逐渐变弱，相似技术企业的溢出效应衰减速度为“先慢后快”，而技术存在差异的企业间溢出效应衰减速度则为“先快后慢”。可见，式(5)进一步丰富和完善了传统研究对溢出效应的设定。
理论模型分为两阶段：第一阶段，企业决定研发投入水平x；第二阶段，企业决定产品产量q。企业在每个阶段都可以选择与对方进行合作或竞争。当企业仅在其中某一个阶段与对方合作时，称为“局部合作”；而如果两阶段都合作时，则为“完全合作”。模型中可能出现的4种情况如表1所示。
表1 4种可能情况
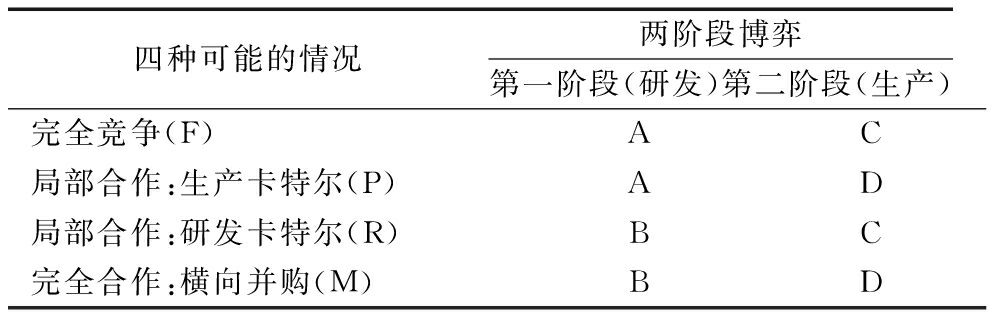
四种可能的情况两阶段博弈第一阶段(研发)第二阶段(生产)完全竞争(F)AC局部合作:生产卡特尔(P)AD局部合作:研发卡特尔(R)BC 完全合作:横向并购(M)BD
注：“A”表示企业在研发阶段相互竞争，独立决定自己的研发投入力度；“B”表示企业在研发阶段进行合作，并通过选择研发投入力度来最大化两企业的利润之和(研发阶段的合作不会改变溢出效应的大小)；“C”表示企业在生产阶段相互竞争；并通过选择产量来最大化自身的利润；“D”表示企业在生产阶段进行合作，最大化两企业的利润之和
(1)完全竞争。在完全竞争情况下，企业在研发与生产阶段均不会合作。通过逆向归纳法(backward induction)，可求得产量qi是关于研发投入xi和xj的表达式，即：
(6)
显然
表明研发投入水平的提高将增加企业产出水平。而对于
则存在以下性质：当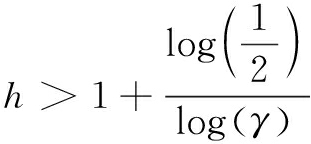
时，
否则，
在第一阶段，每个企业决定各自的研发投入水平以实现利润最大化，完全竞争情况下，可求得研发投入、产量、利润以及社会福利的均衡：
(7)
其中，A=a-c>0，ΨF=4γ+8-γ3-2γ2)+2(γ2h+1+γh+1-2γh-2)>0，ΞF=(γ2-4)2-2(γh+1-2)2>0，ΩF=(48+16γ-24γ2-8γ3+3γ4+γ5)-4(γh+1-2)2>0。
(2)局部合作—生产卡特尔。两企业在研发阶段竞争，而在生产阶段合作。首先，通过最大化两企业联合利润确定第二阶段企业的产量，可得企业i的产出水平为 ：
(8)
可知，
恒为正，而
的正负与h有关：当h<1时，
当h>1时，
利用与前文相似方法求得生产卡特尔情况下的各均衡：
(9)
其中，ΨP=4(1-γ2)+γh(2γ+γh+1-2)+γ-2>0， Ξp=8(γ3-γ2-γ+1)-(γh+1-2)2+4γ-γ2-2γh+2>0，Ωp=12(γ3-γ2-γ+1)-(γh+1-2)2+4γ-γ2-2γh+2>0。
(3)局部合作—研发卡特尔。企业在研发阶段合作而在生产阶段竞争，模型均衡如下所示：
(10)
其中，ΨR=(γ+2)2-2(γh+1)2>0，ΩR=(γ5+11γ4+46γ3+86γ2+64γ+16)+8(γ4h+4γ3h+6γ2h+4γh)-(40γ2h+80γh+2γ2h+3+96γh+1+48γ2h+1+36γh+2+18γ2h+2+4γh+3)>0
(4)完全合作—横向并购。企业在研发和生产两个阶段均进行合作，也可视为两企业间的横向并购。由于两企业生产的产品是不完全替代品，完全合作意味着在每个阶段企业都将最大化他们的联合利润。处于完全合作情况下的企业研发投入、产出、利润和社会福利均衡为：
(11)
其中，ΨM=2(1+γ)-(γh+1)2>0，ΩM=3(1+γ)-(γh+1)2>0
为比较4种情况下研发投入的均衡水平，对fk(γ,h)，gk(γ,h)和jF(γ,h)作如下定义：
fk(γ,h)=xM(γ,h)-xk(γ,h)k={F,P,R}
gk(γ,h)=xR(γ,h)-xk(γ,h)k={F,P}
jF(γ,h)=xP(γ,h)-xF(γ,h)
并在由γ和h构成的二维空间中描绘出fk(γ,h)=0，gk(γ,h)=0，jF(γ,h)=0的曲线。如图2所示，5个区域分别代表了5种不同研发投入水平的排序。
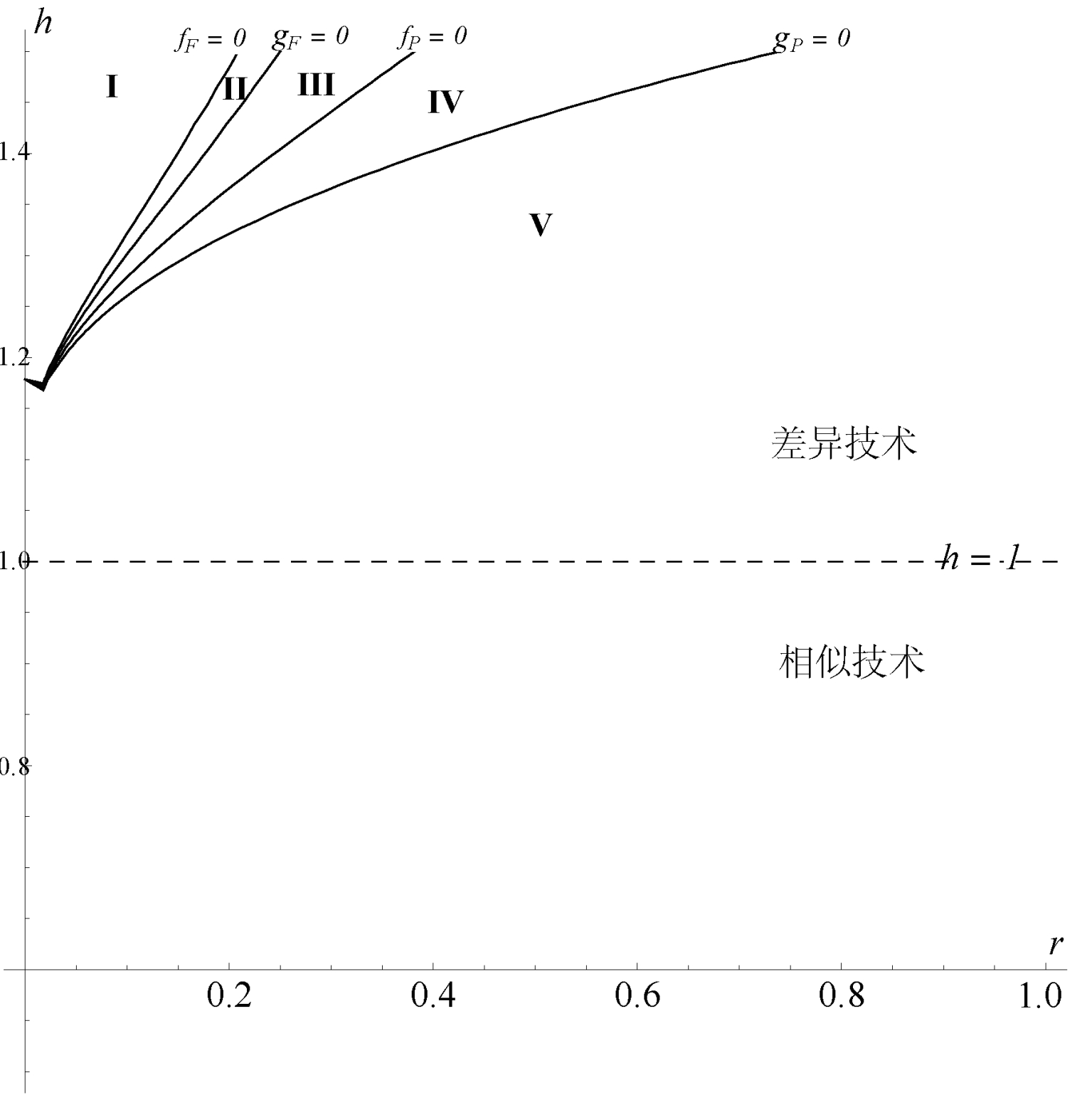
图2 研发投入水平
结论1：区域I：xP>xF>xM>xR；区域II：xP>xM>xF>xR；区域III：xP>xM>xR>xF；区域IV：xM>xP>xR>xF；区域V：xM>xR>xP>xF。
结论1表明，如果企业在研发阶段采取相同策略，在生产阶段选择合作的企业会比选择竞争的企业更有动机对研发活动进行高投入(xM>xR 和xP>xF,∀γ,h)。由于研发投入能够降低生产边际成本并间接引起产品价格下跌，因此当企业在生产阶段合作时，企业就会通过降低产量削弱研发对于产品价格下跌的推动作用。可见，激烈的产品生产竞争消减了研发给企业带来的利益，同时也降低了企业在研发上投资的积极性；而企业在生产阶段的合作对于研发投资具有正向影响，能够激励企业在研发上加大投资力度。不仅如此，如果只考虑技术差距较小的情形(h<1)，企业研发投资水平的排序xM>xR >xP>xF始终保持不变，并且此排序与产品差异的程度无关，这意味着与局部合作相比，企业在完全合作情况下投入在研发上的力度更大。
无论企业在研发阶段采取何种策略行为，生产阶段的合作都会提高他们在研发上的投入，然而企业在研发阶段的合作却并不是总能提高企业研发投入力度。对比完全竞争(情况F)与研发卡特尔(情况R)，不难发现在区域I和II中(高度差异化的产品和较大的技术差距)，研发阶段的合作不利于企业增加研发投入。传统研究认为，在没有考虑产品差异与溢出效应间关系的情况下，完全合作的企业可以独占所有研发创新成果，他们更有意愿在研发方面进行投资，而结论1则证明当企业进行生产卡特尔(情况P)时，企业研发投入力度可能是最大的(区域I、II和III)。
由于模型中的均衡是对称的，产出可看作是衡量消费者剩余的一种指标，即CSk=(1+γ)(qk)2，且k={F,P,R,M}。通过以下曲线将图3分割成几个不同区域。
Rk(γ,h)=qM(γ,h)-qk(γ,h)k={F,P,R}
Vk(γ,h)=qR(γ,h)-qk(γ,h)k={F,P}
ZF(γ,h)=qP(γ,h)-qF(γ,h)
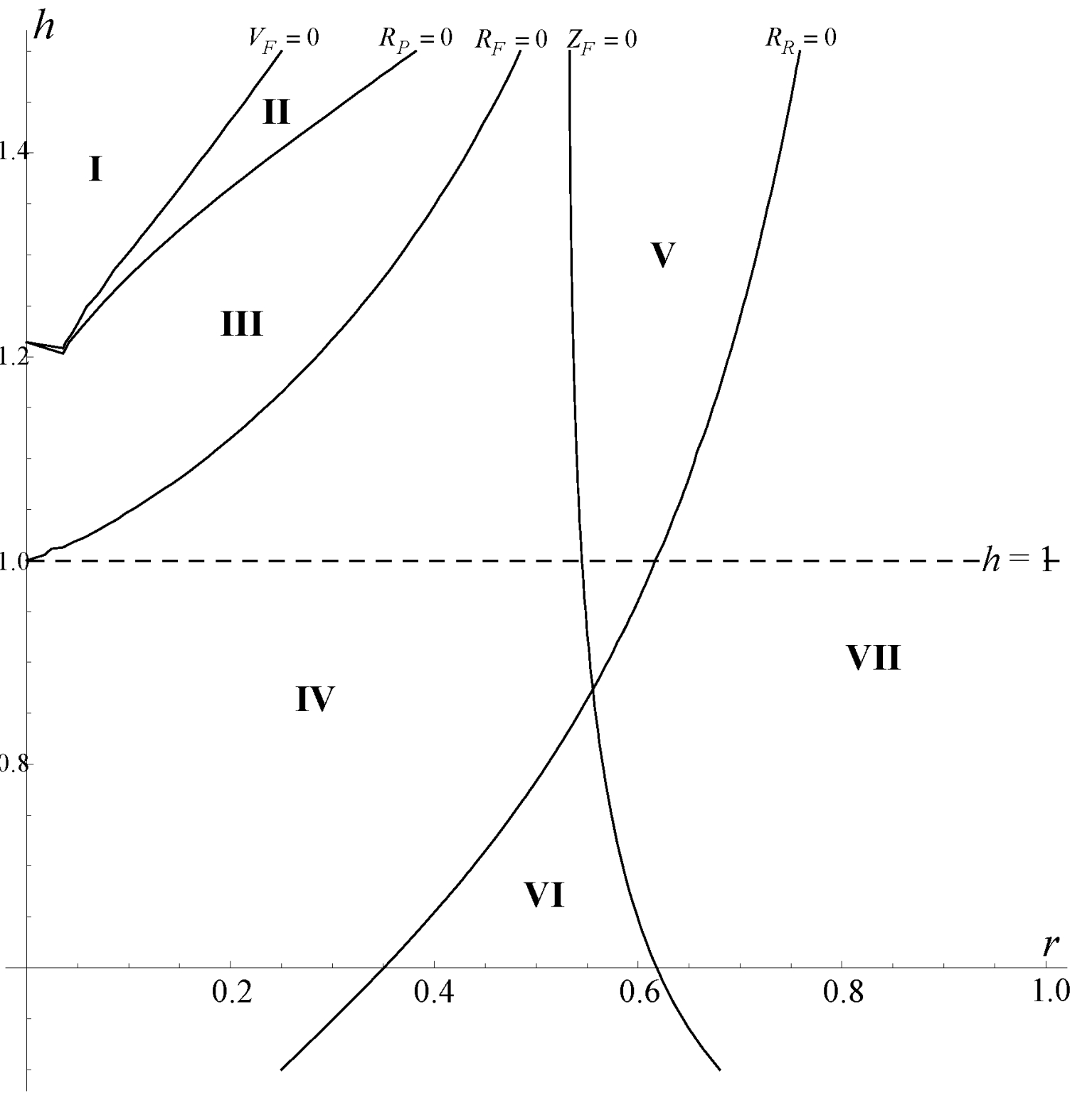
图3 产出(消费者剩余)
结论2 在区域I中qF>qR>qP>qM；在区域II中qR>qF>qP>qM；区域III中qR>qF>qM>qP；区域IV中qR>qM>qF>qP；区域V中qR>qM>qP>qF；区域VI中qM>qR>qF>qP；区域VII中qM>qR>qP>qF。
首先，由结论2可知，对于γ和h的任意取值，qR>qP恒成立。这是因为，一方面在研发卡特尔(R)情况中，研发阶段的合作会加剧生产阶段的竞争；另一方面，在生产卡特尔(P)情况中，企业在生产阶段相互合作，市场竞争的激烈程度大幅降低，因此企业更愿意通过降低产量、提高产品价格增加企业利润。此外，根据图3可知，当企业间的技术差距较小时(h<1)，无论产品差异有多大，就产量而言，在研发阶段进行合作的企业都比在研发阶段采取竞争策略的企业生产得更多，并且采取合作策略的企业也更愿意在研发上进行高投入(参见结论1)。另外，当产品差异较大时(区域I、II和III)，与生产阶段进行合作的企业相比，在该阶段采取竞争策略的企业产量更大。然而，当产品差异较小时(区域VI和VII)，企业在完全合作情况下产量最多，此结果与传统文献中“完全竞争的企业总是比完全合作的企业生产得多”的说法不一致，原因在于传统文献并没有考虑到产品差异与技术差距会影响到溢出效应：较低的差异度会产生较高的溢出效应，并诱使企业在完全合作的情况下加大研发投入(结论1)，从而降低企业的生产边际成本，使完全合作的企业更有动机增加产量。
通过比较各情况下的企业均衡利润水平，可得如下结论：
结论3 (1)πM>max[πP,πR]>min[πP,πR]>πF；(2)当h<1时，πM>πR>πP>πF。
Brod和Shivakumar[31]曾证实某些特殊情况下，企业在完全竞争下的利润可能会比在局部合作下的利润要大。然而，结论3则证实在更具一般化的假设条件下，该论点将不再成立。企业在生产卡特尔中的利润总是高于在完全竞争中获得的利润；而完全合作的企业利润一定大于局部合作的企业利润，且后者的利润大于完全竞争的企业利润。值得注意的是，两种局部合作(生产卡特尔与研发卡特尔)的排序可能会发生变化。
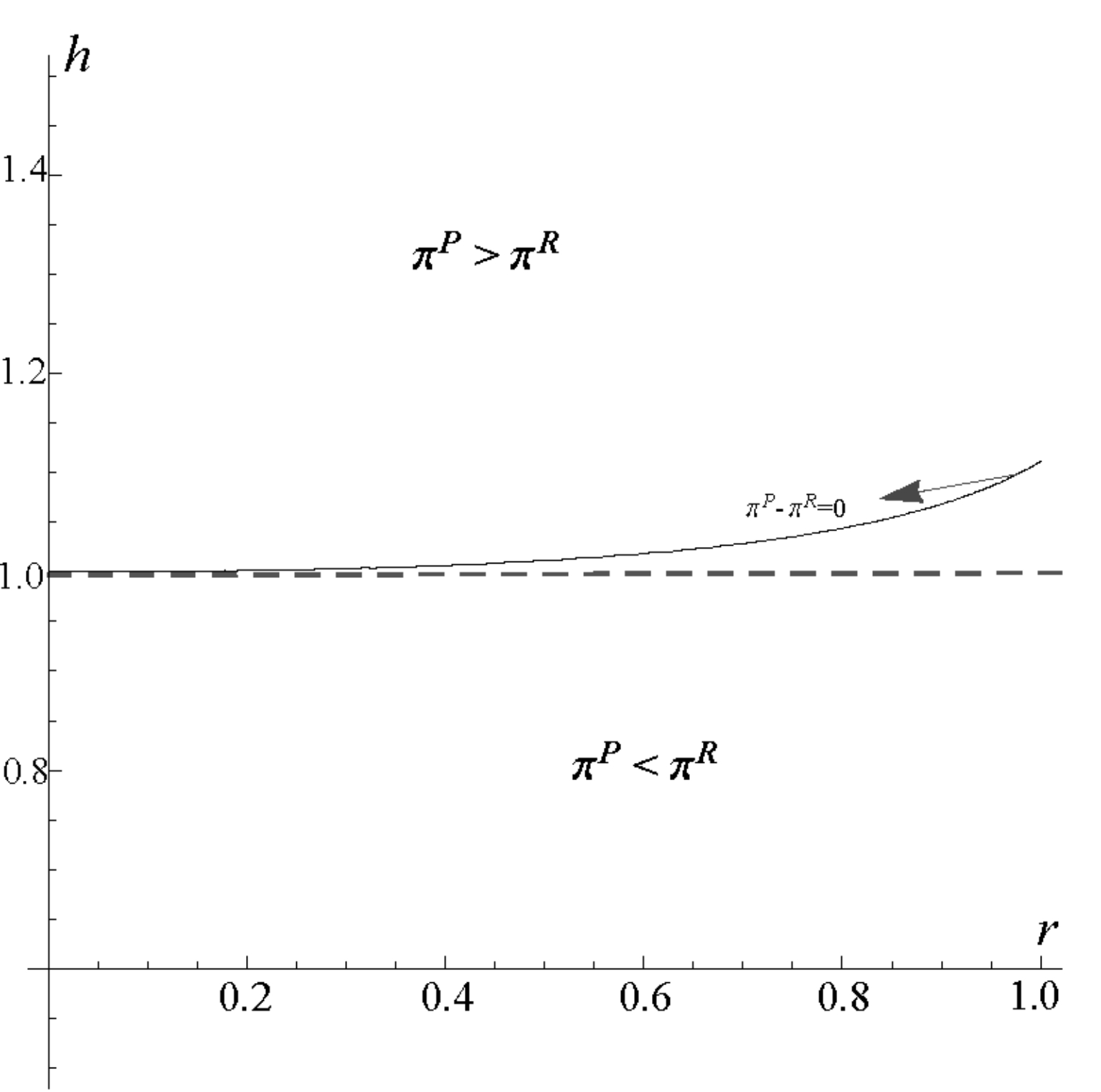
图4 基于两种不同的局部合作的企业利润比较
令Δ表示两种局部合作情况下企业的利润之差，即Δ=πP-πR。从图4可以看出，两种不同的局部合作都可能实现高利润。当技术差距较小时(h<1)，仅在研发阶段合作的企业会比只在生产阶段合作的企业获得更多利润。原因在于较小的技术差距使企业在研发上投入更多(结论1)，由于研发引起生产成本降低，企业就会有更强的竞争力。不仅如此，处于研发卡特尔的企业总是比仅在生产阶段合作的企业生产得更多(结论2)，尽管研发上的投入会带来一定花费，但只要产品差异与溢出效应间呈“凹型”关系，企业在研发卡特尔中获得的收益总比在生产卡特尔中得到的收益来得多。而在“凸型”关系下，结果相反，尤其是当企业间的技术差距足够大时(h>1.12)，较之研发卡特尔，生产卡特尔会有更大优势并给企业带来更多利润。
一般而言，企业合作会降低社会福利水平，尤其是在单一阶段博弈中，合作行为总会损害社会福利。同样，在两阶段博弈中，如果企业在每个阶段都选择合作，则社会福利将降低。本节研究的主要问题是如果将完全竞争情况下的社会福利均衡水平当作参考值，局部或完全合作是否有可能提高社会福利，并且何种合作方式能够使社会福利水平达到最高(参见图5)。
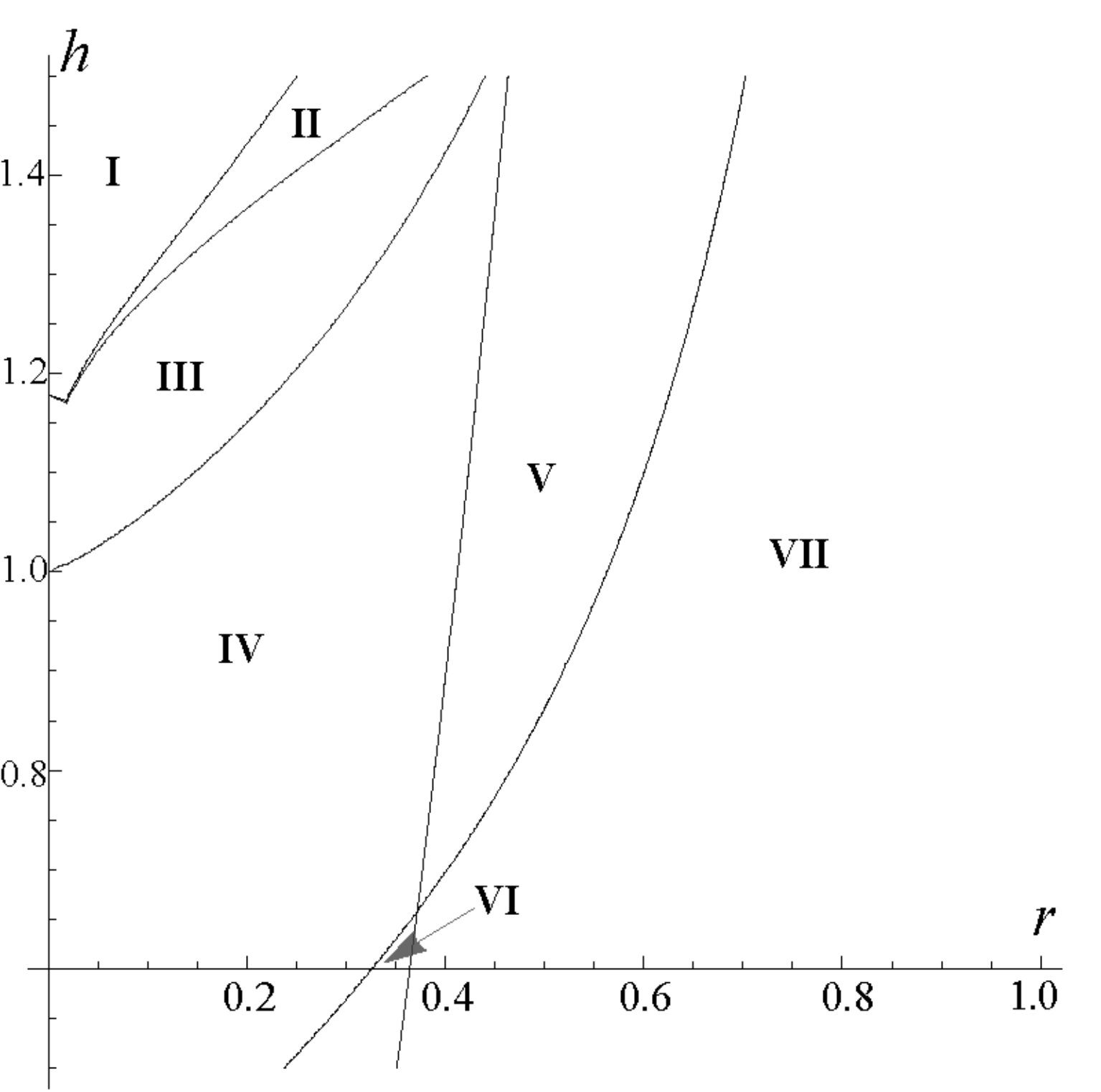
图5 社会福利水平
结论4：区域I中WF>WR>WP>WM；区域II中WR>WF>WP>WM；区域III中WR>WF>WM>WP；区域IV中WR>WM>WF>WP；区域V中WR>WM>WP>WF；区域VI中WM>WR>WF>WP；区域VII中WM>WR>WP>WF。
结论4表明完全合作和局部合作均具有改善社会福利的可能性。例如，当产品差异足够大时，研发卡特尔可以使社会福利达到较高水平，尤其是当企业间技术差距较小时，研发合作企业总比生产合作企业更能有效提高社会福利水平。尽管结论4中各区域的社会福利水平排序和结论2中的排序相同，但二者仍存在不同之处：不同区域所在位置和区域面积大小。对于政府反垄断机构来说，这些不同将会导致消费者福利准则与社会总福利准则出现差异，因此对反垄断政策的讨论就显得尤为必要。
近年来，大多数国家都已经制定了相应的法律法规，要求反垄断机构对企业间的横向并购进行审查。这些反垄断机构通常并不审查并购行为是否会减少竞争(例如美国)或是明显妨碍有效竞争(例如欧盟)，而是以是否影响福利水平以及如何影响为标准。美国与欧盟使用消费者福利标准对并购进行审查；而加拿大、澳大利亚、新西兰等国家多采用社会总福利标准。本节将分别根据消费者福利和社会总福利这两种标准判断并购是否能够通过审核，并且在其中一种标准下被禁止的并购是否能通过另一种标准的审核。
由于在多数国家，生产卡特尔常被政府禁止，因此政府常会选用完全竞争或局部竞争中的研发卡特尔作为参照。如果政府采用社会总福利为衡量标准，当公式(12)成立时，政府机构将批准并购。
WM>max{WF,WR}
(12)
而如果政府采用消费者福利为标准，并购需要满足以下条件才能通过审批。
CSM>max{CSF,CSR}
(13)
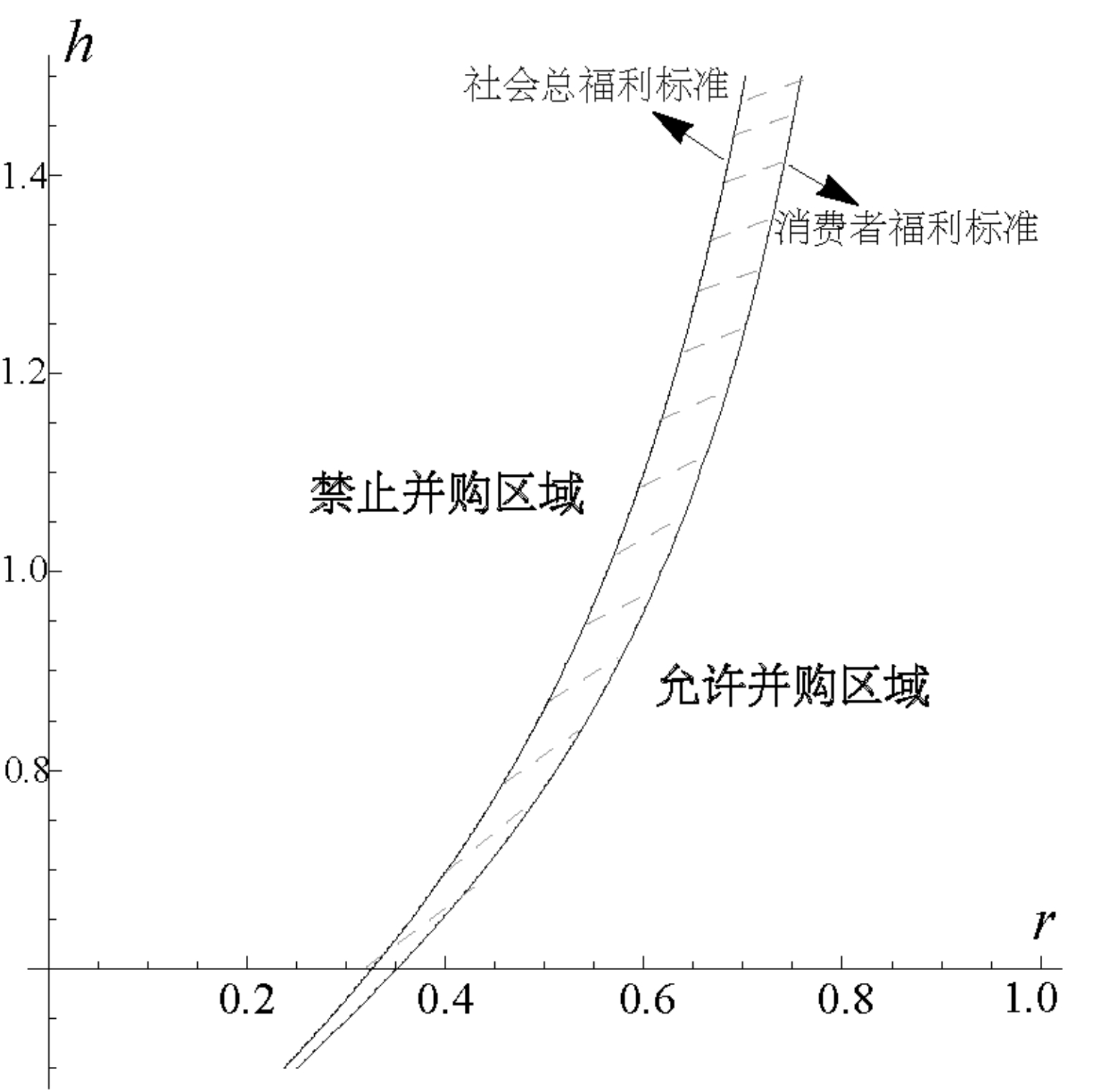
图6 社会总福利标准与消费者福利标准
根据图6可知，“消费者福利标准”曲线右侧部分表示并购可以通过消费者福利标准的审核；同样，“社会总福利标准”曲线右侧区域表示并购可以通过社会总福利标准的审核。两条曲线中间阴影部分则表明在该区域，并购可以通过社会总福利标准审核但无法通过消费者福利标准的审核。除此之外，在曲线左侧区域中，并购是被政府机构所禁止的，企业只能被迫转向利润水平略低的合作方式，因此在此区域内企业会选择研发卡特尔(πR>πF)。
企业是追求经济利益最大化的组织，所以合作联盟成员间的关系并不是单纯的合作关系，其间会存在基于合作基础的竞争合作关系，这就必然会对企业合作的稳定性产生影响。由于联盟内部企业间合作的发展过程类似于重复囚徒困境式合作的进化过程，因此本节将通过一个无限期重复博弈来分析局部合作和完全合作的稳定性。假设企业i背离均衡策略的收益为
上标T表示合作的种类T={R,P,M}，上标D表示企业背离均衡策略。一旦企业i背离均衡，在下一轮博弈中，竞争对手就会通过拒绝合作对企业i进行惩罚。换言之，企业i一旦背离均衡，以后所有参与企业的利润都将是πF。δ表示企业的贴现率(0<δ<1)，企业i在本轮背离后利润的现值为：
(14)
此现值
包括背离均衡的当期利润
加上完全竞争之下今后每期利润的贴现值之和
合作收益则是永远合作的利润现值。令
表示双方合作时企业i的现值，则有
(15)
当下式成立时，企业i会选择放弃合作。
≥
(16)
计算可得：
δ≥
(17)
如果贴现率大于临界值
触发策略可以维持企业的合作关系。反之，当
时，企业就会放弃合作而选择竞争。贴现率的临界值等于当期放弃合作所得的收益除以今后由于企业相互竞争所带来的损失
是合作利润的减函数，也是完全竞争利润πF和背离利润的增函数。换言之，合作的收益越小，对背离的惩罚越轻，背离带来的利润越大，这就需要更大的贴现率来保证企业i不背离“合作之路”。分别对完全合作与两种局部合作(R，P和M)进行分析，可以得到每种情况下贴现率的临界值。
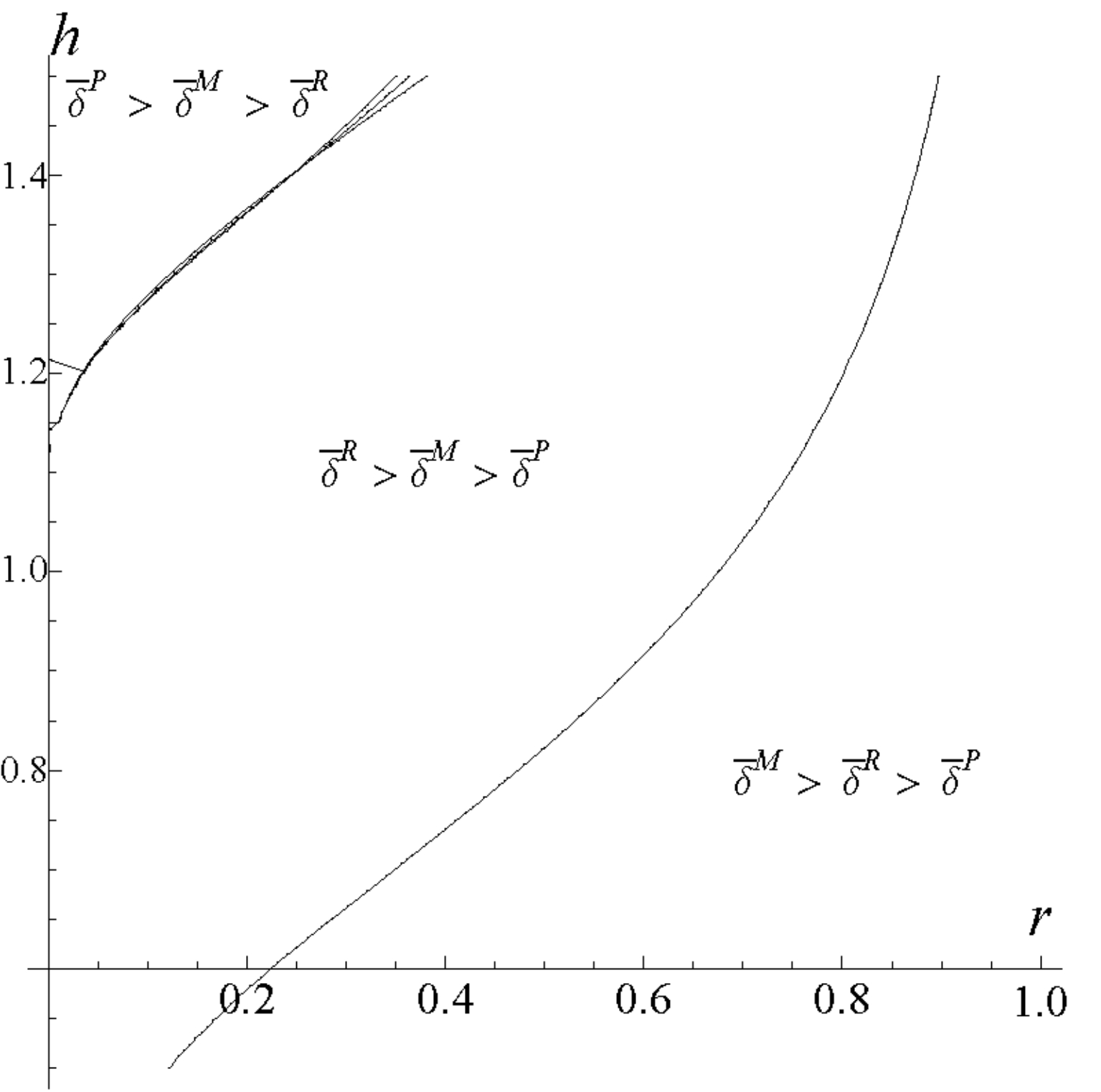
图7 合作方式的稳定性比较
结论5：局部合作比完全合作更加稳定。
由于在生产卡特尔与研发卡特尔中，贴现率的临界值较小，因此与完全合作相比，局部合作更加稳定。不仅如此，当产品差异足够大且技术差距相对较小时，研发阶段的合作最为稳定；而在其它情况下，生产阶段的合作则更加稳定。值得注意的是，图
区域中，完全合作是最不稳定的合作方式。
本文在传统研发溢出效应假设基础上，利用技术差距将溢出效应与产品差异有机联系起来，并通过构建双寡头企业两阶段博弈模型对研发卡特尔、生产卡特尔、完全合作等不同形式合作联盟的均衡水平和福利变化进行了分析和比较。研究证实：
(1) 从促进企业研发投入的角度来看，当企业间技术差距较小时，完全合作策略优于局部合作策略；而当企业间存在较大技术差距且产品高度差异化时，生产卡特尔是最优策略。
(2) 从扩大企业生产规模角度来看，研发卡特尔策略始终优于生产卡特尔策略；当技术差距较小时，企业在研发阶段合作将有利于扩大生产，而如果产品间的差异非常大，企业选择在生产阶段竞争会更益于提高产量。
(3) 从提高企业利润角度来看，完全合作策略始终优于局部合作策略。
(4) 从改善社会福利角度来看，完全合作、研发卡特尔以及完全竞争皆有可能成为企业最优策略；当产品差异较大时，研发卡特尔是改善社会福利的最佳策略。
(5) 从合作稳定性角度来看，局部合作比完全合作更加稳定，尤其是当产品差异足够大且技术差距较小时，研发卡特尔最为稳定。本文研究结论为企业竞争与合作策略行为选择提供了新的理论依据，丰富了该领域的研究成果，同时也拓展了关于溢出效应的传统研究理论。
研究结论有以下政策启示。首先，并不是所有有利可图的企业合作都能改善社会福利，政府一方面可通过补贴、税收减免等政策鼓励和支持合作企业的技术创新，另一方面应对产品市场的竞争状况加以规制，采用限制准入门槛、限制价格等手段对阻碍创新和研发合作的过度竞争进行适度行政及法律干预，以期尽可能抵消企业合作对消费者福利及社会总福利的损害。其次，针对企业合作，政府应进行有目的的引导。企业合作联盟本质上是一种能力互补的竞合关系[32]，政府应结合企业发展特点，为那些技术相关性和互补性强的企业牵线搭桥，从而提高合作联盟研发效率。再次，创新是经济增长的重要动力，但溢出效应过大会导致企业创新动力不足。政府相关部门应加强技术专利和知识产权保护，从而降低全社会的高溢出率，实现从模仿走向创新的重要转变。
本研究尚存在有待拓展之处，后续研究可在以下几方面进行扩展。首先，研发是一种风险较高的活动，可在本模型基础上进一步引入研发不确定性；其次，可进一步检验结论在连续时间动态双头垄断博弈中是否依然成立；再次，本研究中的产品差异是外生变量，而企业可通过控制产品的差异性实现利润最大化，在产品差异内生化的情况下进行研究可能结果会更具意义。
[1] 武丹,管锡展.产业组织角度的合作R&D研究评述[J].产业经济研究,2007(4):62-68.
[2] KATS M L.An analysis of cooperative research and development[J].The Rand Journal of Economics, 1986, 17:527-543.
[3] D'ASPREMONT C, JACQUEMIN A.Cooperative and noncooperative R&D in duopoly with spillovers[J].American Economic Review, 1988, 78:1133-1137.
[4] SUZUMURA K.Cooperative and noncooperative R&D in an oligopoly with spillovers [J].American Economic Review, 1992, 82:1307-1320.
[5] KAMIEN M, MULLER E, ZANG I.Research joint ventures and R&D cartels[J].American Economic Review,1992,82:1293-1306.
[6] ZISS S.Strategic R&D with spillovers, collusion and welfare[J].Journal of Industrial Economics, 1994, 42:375-393.
[7] KABIRAJ T, MUKHERJEE A.Cooperation in R&D and production:a three-firm analysis[J].Journal of Economics, 2000, 71:281-304.
[8] ATALLAH G.Vertical R&D spillovers, cooperation, market structure and innovation[J].Economics of Innovation and New Technology, 2002, 11(3):179-209.
[9] ISHII A.Cooperative R&D between vertically related firms with spillovers[J].International Journal of Industrial Organization, 2004, 22(8-9):1213-1235.
[10] STEPANOVA A, TESORIERE A.R&D with spillovers:monopoly versus noncooperative and cooperative duopoly[J].Manchester School, 2011, 79(1):125-144.
[11] AMIR R, EVSTIGNEEV I, WOODERS J.Noncooperative versus cooperative R&D with endogenous spillover rates[J].Games and Economic Behavior, 2003, 42(2):183-207.
[12] VERSPAGEN B.Measuring intersectoral technology spillovers:estimates from the European and US patent office databases[J].Economic Systems Research, 1997, 9(1):47-65.
[13] AMIR R, WOODERS J.One-way spillovers, endogenous innovator imitator roles, and research joint ventures[J].Games and Economic Behavior, 2000, 31(1):1-25.
[14] HUR K L, WATANABE C.Dynamic process of technology spillover:a transfer function approach[J].Technovation, 2002, 22(7):437-444.
[15] PIGA C, POYAGO-THEOTOKY J.Endogenous R&D spillovers and locational choice [J].Regional Science and Urban Economics,2005,35:127-139.
[16] DEY S, FU Q.Do firms value knowledge spillover? a model of R&D competition, endogenous R&D appropriability and product differentiation [C].National University of Singapore Working Paper，2009:1-31.
[17] 武博,陈萱源,陈颖.纵向溢出效应对企业独立研发与纵向RJV的影响研究[J].科学学与科学技术管理,2011,32(2):14-19.
[18] 赵凯.信息不对称时产业链企业研发投资行为及产业集群效应分析[J].产业经济研究, 2015(4):21-31.
[19] 丁旭,孟卫东,陈晖.基于技术风险的供应链纵向合作研发利益分配方式研究[J].科技进步与对策,2011,28(20):19-23.
[20] 赵麟,石岿然,黄芳.具有溢出效应的纵向R&D合作[J].科技进步与对策,2009, 26(7):112-114.
[21] 陈宇科,邹艳,杨洋.基于产品生命周期和溢出效应的企业合作研发策略[J].中国管理科学,2013,21(11):570-575.
[22] 生延超.创新投入补贴还是创新产品补贴:技术联盟的政府策略选择[J].中国管理科学,2008,16(6):184-192.
[23] 游达明,朱桂菊.不同竞合模式下企业生态技术创新最优研发与补贴[J].中国工业经济,2014(8):122-134.
[24] 但斌,田丽娜,董绍辉.考虑溢出效应的互补品企业间广告决策模型研究[J].中国管理科学,2013,21(2):66-75.
[25] 茆训诚.基于技术溢出效应和产品差异化视角的企业研发组织模式动态选择研究[J].上海经济研究,2009(1):3-12.
[26] 石光.技术互补性、产品可替代性与企业研发合作[J].管理科学,2012,25(5):22-29.
[27] 侯光明,艾凤义.基于混合一处的双寡头横向R&D合作[J].管理科学学报,2006,20(4):94-97.
[28] 苏素,肖阿妮.基于混合溢出效应的产业共性技术研发组织模式研究[J].科技进步与对策,2012,29(5):23-28.
[29] 张春辉,陈继祥.考虑内生溢出与R&D投入的创新模式选择[J].中国管理科学,2011, 19(3):26-32.
[30] 刘金平,黄波,李宇雨.基于投资溢出的并行研发联盟成员的投资策略实验研究[J].科技进步与对策,2011,28(2):9-12.
[31] BROD A, SHIVAKUMAR R.Advantageous semi-collusion [J].Journal of Industrial Economics, 1999, 47(2):221-230.
[32] 何慧爽.产品差异化、竞争强度与企业R&D策略分析[J].科学学研究,2010,28(9):1361-1367.
开放科学(资源服务)标识码(OSID)：